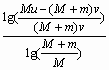题目内容
一个质量为M的雪橇静止在水平雪地上,一条质量为m的爱斯基摩狗站在雪橇上.狗向雪橇的正后方跳下,随后又追赶并向前跳上雪橇;其后狗又反复地跳下、追赶并跳上雪橇.狗与雪橇始终沿一条直线运动.若狗跳离雪橇时雪橇的速度为V,则此时狗相对于地面的速度为V+u(其中u为狗相对于雪橇的速度,V+u为代数和,若以雪橇运动的方向为正方向,则V为正值,u为负值.)设狗总以速度v追赶和跳上雪橇,雪橇与雪地间的摩擦忽略不计.已知v的大小为5 m/s,u的大小为4 m/s,M=30 kg,m=10 kg.
(1)求狗第一次跳上雪橇后两者的共同速度的大小.
(2)求雪橇最终速度的大小和狗最多能跳动上雪橇的次数.
(供使用但不一定用到的对数值:lg2=0.301,lg3=0.477)
解析:
|
(1)设雪橇运动的方向为正方向,狗第1次跳下雪橇后雪橇的速度为V1,根据动量守恒定律,有 狗第1次跳上雪橇时,雪橇与狗的共同速度为 可解得 将u=-4 m/s,v=5 m/s,M=30 kg,m=10 kg代入,得 (2)解法(一) 设雪橇运动的方向为正方向,狗第(n-1)次跳下雪橇后雪橇的速度为 这样,狗n次跳下雪橇后,雪橇的速度为Vn,满足 解得 狗追不上雪橇的条件是Vn≥v 可化为 最后可求得n≥1+ 代入数据,得n≥3.41 狗最多能跳上雪橇3次. 雪橇最终的速度大小为V4=5.625 m/s 解法(二): 设雪橇运动的方向为正方向,狗第i次跳下雪橇后,雪橇的速度为Vi,狗的速度为 第一次跳下雪橇: 第一次跳上雪橇: 第二次跳下雪橇: 第三次跳下雪橇: 第三次跳上雪橇 第四次跳下雪橇: 此进雪橇的速度已大于狗追赶的速度,狗将不可能追上雪橇.因此狗最多能跳上雪橇3次,雪橇最终的速度大小为5.625 m/s. |