题目内容
【题目】如图所示，质量m=2.6kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动．（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：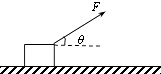
（1）金属块与地板间的动摩擦因数；
（2）若在运动过程的某一时刻保持力F的大小不变，突然将力的方向变为水平向右，这一时刻金属块的加速度大小为多少？
（3）若在匀速直线运动某一时刻撤去力F，金属块再经过多长时间停下来？
【答案】
（1）
解：设地板对金属块的支持力为FN，金属块与地板的动摩擦因数为μ，因为金属块匀速运动，所以有：
Fcosθ=μFN
mg=Fsinθ+FN
解得： 
（2）
解：由牛顿第二定律得：
F﹣μmg=ma1
代入数据解得：a1= 
m/s2≈﹣0.154m/s2
负号表示加速度方向与速度方向相反，大小为0.154m/s2
（3）
解：撤去力F后有：μmg=ma2
代入数据有：a2=4m/s2
由t= 
代入数据解得：t=1.25s
【解析】（1）根据共点力平衡求出金属块与地板间的动摩擦因数．（2）根据牛顿第二定律，结合物体所受的合力求出金属块的加速度．（3）撤去拉力后，根据牛顿第二定律求出加速度，结合速度时间公式求出金属块到停止的时间．
阅读快车系列答案【题目】根据课本中“探究加速度与力、质量的关系”的实验，回答下列问题．
（1）本实验应用的实验方法是法，下列说法中正确的是 ．
A．在探究加速度与质量的关系时，应该改变拉力的大小
B．在探究加速度与外力的关系时，应该改变小车的质量
C．在探究加速度a与质量m的关系时，为了直观判断二者间的关系，应作出a= 
图象
D．当小车的质量远大于砝码盘和砝码的总质量时，才能近似认为细线对小车的拉力大小等于砝码盘和砝码的总重力大小
（2）某同学测得小车的加速度a和拉力F的数据如表所示：（小车质量保持不变）
F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
a/（ms2） | 0.10 | 0.20 | 0.28 | 0.40 | 0.52 |
①根据表中的数据在如图的坐标图上作出a﹣F图象 ．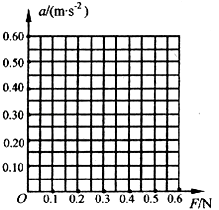 
②产生实验误差的原因可能是 ．
