��Ŀ����
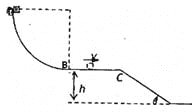
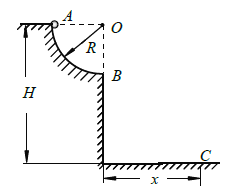
����Ŀ����ͼ��ʾ��λ����ֱƽ���ڵ�1/4 Բ���⻬������뾶ΪR���������͵�B ��������ˮƽ������϶�A ��ˮƽ����߶�ΪH������Ϊm ��С����Ϊ�ʵ㣩�ӹ�����϶�A ���ɾ�ֹ�ͷţ���������¶�B ��ˮƽ�ɳ����������ˮƽ�����ϵ�C �㴦�������������ɺ��Բ��ƣ��������ٶ�Ϊg����
��1��С���˶���B ��ʱ�����������֧������
��2��С����ص�C ��B ���ˮƽ����x��
��3����ֵR/H Ϊ����ʱ��С����ص�C ��B ��ˮƽ����x ��Զ���������ˮƽ���룮
���𰸡���1��3mg ��2��2![]() ��3��
��3��![]() H����2R��
H����2R��
��������
���⣨1��С���A���˶���B��Ĺ����У���е���غ㣬����B����ٶ�ΪvB�����ݻ�е���غ㶨���У�
mgR=![]() mvB2(2�֣�
mvB2(2�֣�
��С����B��ʱ���ܹ����֧����ΪFN����С����B�����ţ�ٵڶ������У�
FN-mg=m![]() (2�֣�
(2�֣�
�����ɽ�ã�
FN=3mg ��1�֣�
��2��С���뿪B�����ƽ���˶���
����ֱ�����У�
H-R��![]() ��2�֣�
��2�֣�
��ˮƽ�����У�
x=vB t ��2�֣�
������ã�
x=2![]() ��1�֣�
��1�֣�
��3����x=2![]() �ɵ�����
�ɵ�����
x=![]()
��![]() ʱ��x�����ֵ ��1�֣�
ʱ��x�����ֵ ��1�֣�
x�����ֵ��xm=H����xm=2R��

��ϰ��ϵ�д�
�����Ŀ