题目内容
一人手里抓住一根长为L的轻质细绳的一端,绳的另一端系着一个质量为m的小球,若要使小球能在竖直面内作圆周运动,它过最高点时的角速度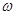 应满足的条件是:
应满足的条件是:
A.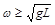 | B.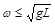 | C. | D. |
C
解析试题分析:对小球在最高点进行受力分析,要注意绳子对小球只能提供向下的拉力,临界状态就是当绳子的作用力刚好为零时,此时重力提供向心力,小球的速度取最小值,此时它转动的角速度ω也取最小值.
对小球在最高点进行受力分析,合力提供向心力,则 ,当FN=0时小球的角速度取最小值,故
,当FN=0时小球的角速度取最小值,故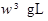 故选C.
故选C.
考点:牛顿第二定律;向心力.
点评:该题是圆周运动向心力公式的直接应用,要抓住恰好到达最高点的隐含条件是由重力来提供向心力,难度不大,属于基础题.

练习册系列答案
相关题目
 应满足的条件是:
应满足的条件是: ; B.
; B. ; C.
; C. ; D.
; D. 。
。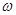 应满足的条件是:
应满足的条件是: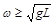 B.
B.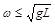 C.
C.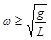 D.
D.