题目内容
9. 竖直放置在大气压恒为p0的空气中的圆柱形容器内用质量为m的活塞密封一部分气体,活塞与容器壁间能无摩擦滑动,容器的横截面积为S.开始时气体的温度为T0,活塞与容器底的距离为h0.当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,求:
竖直放置在大气压恒为p0的空气中的圆柱形容器内用质量为m的活塞密封一部分气体,活塞与容器壁间能无摩擦滑动,容器的横截面积为S.开始时气体的温度为T0,活塞与容器底的距离为h0.当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,求:(1)吸收热量后气体的温度是多少?
(2)在此过程中的密闭气体的内能增加了多少?
分析 (1)在气体的温度升高的过程中,气体的压强不变,利用盖•吕萨克定律即可解得吸收热量后气体的温度.
(2)该过程气体的压强不变,所以气体对外所做的功可用气体作用在活塞上的力与活塞移动的距离的乘积表示,再结合热力学第一定律即可得知内能的增加.
解答 解:(1)取封闭气体为研究对象,活塞上升过程为等压变化,
状态1:V0=h0S,温度为T0
状态2:V=(h0+d)S,温度设为T
由盖•吕萨克定律有:$\frac{V}{{V}_{0}}=\frac{T}{{T}_{0}}$
得吸收热量后气体的温度:T=$\frac{{h}_{0}+d}{{h}_{0}}{T}_{0}$
(2)活塞上升的过程,密闭气体客服大气压和活塞的重力做功,所以外界对系统做的功为:
W=-(mg+P0S)d
根据热力学第一定律得密闭气体增加的内能为:
△E=Q+W=Q-(mg+P0S)d
答:(1)吸收热量后气体的温度是$\frac{{h}_{0}+d}{{h}_{0}}{T}_{0}$;
(2)在此过程中的密闭气体的内能增加了Q-(mg+P0S)d
点评 该题首先考查了理想气体状态方程的应用,要首先对要研究的气体进行状态的分析和状态参量的分析,尤其要注意对压强的分析,再根据状态变化的特点选择合适的定律进行解答.该题还考察了热力学第一定律的应用,当压强不变时,可用气体对活塞的作用力与活塞移动的距离来定量计算做功情况,同时要注意做功和热量的正负

练习册系列答案
相关题目
19.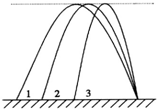 如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
 如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )| A. | 沿路径1抛出的物体落地的速率最大 | |
| B. | 沿路径3抛出的物体在空中运动的时间最长 | |
| C. | 沿路径3抛出的物体初速度的竖直分量最大 | |
| D. | 三个物体抛出时初速度的水平分量相等 |
20. 轻杆的一端安装有一个小滑轮P,用手握住杆的另一端支撑着悬挂重物的轻绳,如图所示.现使杆和竖直方向的夹角缓慢减小,则下列关于杆对滑轮P的作用力的下列判断正确的是( )
轻杆的一端安装有一个小滑轮P,用手握住杆的另一端支撑着悬挂重物的轻绳,如图所示.现使杆和竖直方向的夹角缓慢减小,则下列关于杆对滑轮P的作用力的下列判断正确的是( )
 轻杆的一端安装有一个小滑轮P,用手握住杆的另一端支撑着悬挂重物的轻绳,如图所示.现使杆和竖直方向的夹角缓慢减小,则下列关于杆对滑轮P的作用力的下列判断正确的是( )
轻杆的一端安装有一个小滑轮P,用手握住杆的另一端支撑着悬挂重物的轻绳,如图所示.现使杆和竖直方向的夹角缓慢减小,则下列关于杆对滑轮P的作用力的下列判断正确的是( )| A. | 变大 | B. | 不变 | C. | 变小 | D. | 无法确定 |
17.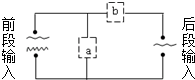 在电子线路中,经天线接收下来的电信号既有高频成分又有低频成分,需要把低频成分和高频成分分开,只让低频成分输送到下一级,可以采用如图所示的电路,其中a、b应选择的元件是( )
在电子线路中,经天线接收下来的电信号既有高频成分又有低频成分,需要把低频成分和高频成分分开,只让低频成分输送到下一级,可以采用如图所示的电路,其中a、b应选择的元件是( )
 在电子线路中,经天线接收下来的电信号既有高频成分又有低频成分,需要把低频成分和高频成分分开,只让低频成分输送到下一级,可以采用如图所示的电路,其中a、b应选择的元件是( )
在电子线路中,经天线接收下来的电信号既有高频成分又有低频成分,需要把低频成分和高频成分分开,只让低频成分输送到下一级,可以采用如图所示的电路,其中a、b应选择的元件是( )| A. | a是电容较大的电容器,b是低频扼流圈 | |
| B. | a是电容较大的电容器,b是高频扼流圈 | |
| C. | a是电容很小的电容器,b是低频扼流圈 | |
| D. | a是电容很小的电容器,b是高频扼流圈 |
4.下列说法中正确的是( )
| A. | 研究地球绕太阳的运动时地球可视为质点 | |
| B. | 相对于不同的参考系来描述同一个物体的运动其结果可能不同 | |
| C. | 上午第一节课8:00上课,8:00是时间间隔 | |
| D. | 路程和位移是相同的物理量 |
14.下列说法正确的是( )
| A. | α粒子散射实验中少数α粒子发生了较大偏转,这是卢瑟福猜想原子核式结构模型的主要依据之一 | |
| B. | 在光电效应实验中,用同种频率的光照射不同的金属表面,从金属表面逸出的光电子的最大初动能Ek越大,则这种金属的逸出功W0越大 | |
| C. | 用能量等于氘核结合能的光子照射静止氘核,不可能使氘核分解为一个质子和一个中子 | |
| D. | 某放射性原子核经过2次α衰变和一次β衰变,核内中子数减少4个 | |
| E. | 一个中子与一个质子发生核反应,生成一个氘核,其核反应方程式为${\;}_{0}^{1}$n+${\;}_{1}^{1}$H→${\;}_{1}^{2}$H;若该反应放出的能量为Q,则氘核的比结合能为$\frac{Q}{2}$ |
18. A、B两带电小球,质量分别为mA、mB,电荷量分别为qA、qB,用绝缘不可伸长的细线如图悬挂,静止时A、B两球处于同一水平面.若B对A及A对B的库仑力分别为FA、FB,则下列判断正确的是( )
A、B两带电小球,质量分别为mA、mB,电荷量分别为qA、qB,用绝缘不可伸长的细线如图悬挂,静止时A、B两球处于同一水平面.若B对A及A对B的库仑力分别为FA、FB,则下列判断正确的是( )
 A、B两带电小球,质量分别为mA、mB,电荷量分别为qA、qB,用绝缘不可伸长的细线如图悬挂,静止时A、B两球处于同一水平面.若B对A及A对B的库仑力分别为FA、FB,则下列判断正确的是( )
A、B两带电小球,质量分别为mA、mB,电荷量分别为qA、qB,用绝缘不可伸长的细线如图悬挂,静止时A、B两球处于同一水平面.若B对A及A对B的库仑力分别为FA、FB,则下列判断正确的是( )| A. | FA<FB | |
| B. | 细线OC的拉力FTC=(mA+mB)g | |
| C. | 细线AC对A的拉力FTA=$\frac{{m}_{A}}{2}$g | |
| D. | 同时烧断细线AC、BC后,A、B在竖直方向的加速度相同 |

 如图所示,质量M=4kg的木板静置于光滑水平面上,质量m=1kg的小物块(可视为质点)以初速度v0=4m/s从木板的左端冲上木板,同时在木板的右端施加一个水平向右F=2N的恒力,经t=1s撤去外力,最后小物块恰好不从木板的上端滑下,已知小物块与木板之间的动摩擦因数μ=0.2,重力加速度g=10m/s2,求:
如图所示,质量M=4kg的木板静置于光滑水平面上,质量m=1kg的小物块(可视为质点)以初速度v0=4m/s从木板的左端冲上木板,同时在木板的右端施加一个水平向右F=2N的恒力,经t=1s撤去外力,最后小物块恰好不从木板的上端滑下,已知小物块与木板之间的动摩擦因数μ=0.2,重力加速度g=10m/s2,求: