题目内容
（2013?琼海模拟）如图所示，某种透明液体的折射率为n，在液面下深为h处有一点光源S，现有一不透光的圆形薄板置于液面，其圆心O在S的正上方．要使观察者从液面上任一位置都不能看到点光源S，则该圆形薄板的半径R至少为多大？分析：心O在S的正上方，恰好从液面上任一位置都不能看到点光源S．知由光源S射出的光在薄片的边缘发生全反射，根据sinC=
求出临界角，然后由几何知识求出求出圆形薄板的半径R．
| 1 |
| n |
解答：解：全反射的临界角sinC=
，
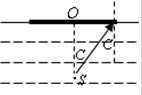
则tanC=
即：
=
得：R=
答：圆形薄板的半径R至少为
．
| 1 |
| n |
则tanC=
| 1 | ||
|
即：
| R |
| h |
| 1 | ||
|
得：R=
| h | ||
|
答：圆形薄板的半径R至少为
| h | ||
|
点评：解决本题的关键知道临界角和折射率的关系，并画出恰好发生全反射时的光路图．
练习册系列答案
相关题目
（2013?琼海模拟）如图，在场强为E的匀强电场中有一个质量为m的带正电小球A悬挂在绝缘细线上，当小球静止时，细线与竖直方向成θ=30°角，已知此电场方向正好与OA垂直，则小球所带的电量应为（ ）
（2013?琼海模拟）如图所示，质量为m=0.1kg的物体放在升降机底部，一根竖直弹簧上端固定在升降机顶部，下端连接物体，当升降机以4m/s2的加速度加速向上运动时，弹簧对物体的拉力为0.4N；当升降机以8m/s2的加速度加速向上运动时，弹簧的拉力为（ ）