题目内容
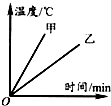 用两个相同的加热器,分别对质量相等的甲、乙两种液体加热,其温度随时间变化的图线如图所示,由图线可以看出( )
用两个相同的加热器,分别对质量相等的甲、乙两种液体加热,其温度随时间变化的图线如图所示,由图线可以看出( )分析:选同样的加热时间,甲和乙吸热相同,根据温度变化的多少判断,温度变化多的比热容小,温度变化少的比热容大,据此分析判断.
解答:解:A、B、C、由图示可以看出,当加热时间相同时,即吸收的热量相同时,甲的温度升高的快,利用热量的计算公式Q吸=cm△t可知,在质量相等、初温相同、吸热也相同的情况下,谁的温度升高得快,它的比热容小;
所以,甲的比热容小,乙的比热容大.故AC错误,B正确.
D、比热容与物体的温度无关,有物体的材料决定.故D错误.
故选B.
所以,甲的比热容小,乙的比热容大.故AC错误,B正确.
D、比热容与物体的温度无关,有物体的材料决定.故D错误.
故选B.
点评:本题考查了学生对比热容了解与掌握,注意要学会看图形(取相同的时间比较甲乙温度变化的高低).

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 分享到
分享到- QQ空间
- 新浪微博
- 百度搜藏
- 人人网
- 腾讯微博
- 开心网
- 腾讯朋友
- 百度空间
- 豆瓣网
- 搜狐微博
- MSN
- QQ收藏
- 我的淘宝
- 百度贴吧
- 搜狐白社会
- 更多...
百度分享
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:电磁打点计时器、米尺、纸带、复写纸片。
实验步骤:
(1)如图1所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上。
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
(3)经过一段时间,停止转动和打点,取下纸带,进行测量。
① 由已知量和测得量表示的角速度的表达式为ω= 。式中各量的意义是:
.
② 某次实验测得圆盘半径r=5.50×10-2m,得到纸带的一段如图2所示,求得角速度为 。
(1) (2)6.8/s。 |
 的油酸酒精溶液逐滴滴入量筒,记下
的油酸酒精溶液逐滴滴入量筒,记下 。
。 (3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将
(3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将 (2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是
(2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是 (3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针
(3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针 (1)下列说法中正确的是___▲_____
(1)下列说法中正确的是___▲_____  (3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端
(3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端
 的内容及实验步骤
的内容及实验步骤 中的计算式:
中的计算式: 的油酸酒精溶液逐滴滴入量筒,记下
的油酸酒精溶液逐滴滴入量筒,记下 的油酸酒精溶液的滴数
的油酸酒精溶液的滴数 ;
; ;
; 的正方形为单位,计算轮廓内正方形的个数
的正方形为单位,计算轮廓内正方形的个数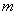 ;
; __▲____
__▲____ 。
。 (3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将
(3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将 (2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是
(2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是 (3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针
(3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针 、
、 确定入射光线,并让入射光线过圆心
确定入射光线,并让入射光线过圆心 ,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针
,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针 ,使
,使 。图中
。图中 为分界面,虚线半圆与玻璃砖对称,
为分界面,虚线半圆与玻璃砖对称, 、
、 、
、 均垂直于法线并分别交法线于
均垂直于法线并分别交法线于 、
、 点。设
点。设 ,
, 的长度为
的长度为 ,
, ,
, 的长度为
的长度为 ,求:
,求: (1)下列说法中正确的是___▲_____
(1)下列说法中正确的是___▲_____  (3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端
(3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端