题目内容
【题目】从斜面上某位置，每隔0.1s释放一个小球，在连续释放几个后，对在斜面上的小球拍下照片，如图所示，测得sAB=18cm，sBC=20cm，试求
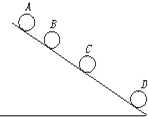
（1）小球的加速度．
（2）拍摄时B球的速度vB=？
（3）拍摄时sCD=？
（4）A球上面滚动的小球还有几个？
【答案】（1）小球的加速度为2m/s2
（2）拍摄时B球的速度vB为1.9m/s；
（3）拍摄时SCD为0.22m；
（4）A球上面滚动的小球还有8个．
【解析】
试题分析：（1）匀变速直线运动中，在连续相等时间内的位移之差是一恒量，即△s=aT2，根据该推论求出小球的加速度．
（2）某段时间内的平均速度等于中间时刻的瞬时速度，B点是AC两点的中间时刻，求出AC段的平均速度，即可知道B球的速度．
（3）在连续相等时间内的位移之差是一恒量，有sCD﹣sBC=sBC﹣sAB．根据该关系CD间的距离．
（4）根据速度时间公式求出A球的速度，从而得出A球运动的时间，根据A球的时间确定A球上面滚动球的个数．
解析：（1）由△s=aT2，知小球的加速度为：
a=
=
cm/s2=200 cm/s2=2 m/s2
（2）B点的速度等于AC段的平均速度即：
vB=
=
cm/s=1.9 m/s
（3）由于相邻相等时间的位移差恒定即：
sCD﹣sBC=sBC﹣sAB
所以有：sCD=2sBC﹣sAB=（40﹣18）cm=22 cm=0.22 m
（4）设A点小球的速率为vA，因为：
vB=vA+at，vA=vB﹣at=1.9﹣2×0.1=1.7 m/s
所以A球的运动时间为：tA=
=
s=0.85 s，故A球的上方正在滚动的小球还有8个．
答：（1）小球的加速度为2m/s2
（2）拍摄时B球的速度vB为1.9m/s；
（3）拍摄时SCD为0.22m；
（4）A球上面滚动的小球还有8个．
