题目内容
17.现有A、B两列火车在同一轨道上同向行驶,A车在前,其速度vA=10m/s,B车速度vB=30m/s.因大雾能见度低,B车在距A车600m时才发现A车,此时B车立即刹车,但B车要减速1800m才能够停止.(1)求B车刹车后减速运动的加速度多大?
(2)A车若仍按原速度前进,两车是否会相撞?若会相撞,将在何时何地发生?
(3)若B车刹车8s后,A车以加速度a1=0.5m/s2加速前进,问能否避免事故?若能够避免则两车最近时相距多远?
分析 (1)根据B车刹车,要经过1800m才能停止,由速度位移公式求出B车的加速度.
(2)(3)B车刹车做匀减速运动,当速度减至与A车相等时,如果没有追上A车,则两车不会相撞;若两车速度相等,B车追上了A车,则两车会相撞.根据两车速度时位移关系,判断两车能否相撞.速度相等时不碰撞以后就不会碰撞了,先根据公式求得经过多长时间两车速度相等,两车的位移之差即为所求得距离
解答 解:(1)设B车减速运动的加速度大小为a,有:0-vB2=-2ax1,
代入数据解得:a=0.25 m/s2.
(2)设B车减速t秒时两车的速度相同,有:vB-at=vA
解得t=80s
在此过程中B车前进的位移为:
xB=vBt-$\frac{1}{2}a{t}^{2}$=30×$80-\frac{1}{2}×0.25××8{0}^{2}$=1600m
A前进位移为xA=vAt=10×80=800m
由于800+600<1600m,故两车会相撞
设相撞时间为t0,则根据vBt0-$\frac{1}{2}$at${\;}_{0}^{2}$=600+vAt0
解得t0=40s
此时A位移为xA=vAt0=10×40=400m
(3)设B车减速t秒时两车的速度相同,有:vB-at=vA+a1(t-△t),
代入数值解得:t=32s,
在此过程中B车前进的位移为:
xB=vBt′-$\frac{1}{2}$at′2
代入数据解得:xB=832m,
A车前进的位移为:
xA=vA△t+vA(t-△t)+$\frac{1}{2}$a1(t-△t)2,
代入数据解得:xA=464m,
因xA+x>xB,故不会发生撞车事故,此时△x=xA+x-xB=232 m.
答:(1)B车刹车后减速运动的加速度为0.25m/s2.
(2)A车若仍按原速度前进,两车是会相撞,将在40s距A起始点400m处.
(3)若B车刹车8s后,A车以加速度a1=0.5m/s2加速前进,能避免事故,两车最近时相距232m
点评 解决本题的关键知道速度大者减速追速度小者,在速度相等之前,两车的距离越来越小,若未相撞,速度相等之后,两车的距离越来越大,可知只能在速度相等之时或相等之前相撞.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | 从北京开往广州的火车预计10时到站 | |
| B. | 1997年7月1日零时中国对香港恢复行驶主权 | |
| C. | 某人百米跑的成绩是13s | |
| D. | 某场足球开赛了15min时甲队攻入一球 |
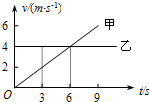
| A. | t=0时乙在甲的前方9 m处 | B. | t=0时甲在乙的前方9 m处 | ||
| C. | 3s之后两物体还会再相遇 | D. | 3 s之后两物体不会再相遇 |
| A. | 做匀速圆周运动的物体受到的外力突然变大的运动 | |
| B. | 做匀速圆周运动的物体受到的外力突然变小的运动 | |
| C. | 做匀速圆周运动的物体受到的外力突然消失的运动 | |
| D. | 物体受到的离心力大于向心力时,物体做离心运动 |
 如图所示,水平恒力F拉着质量为m的木块在水平放置在地面上的长木板上向右匀速运动,木板恰好能保持静止.则在此基础上,再逐渐增大F的过程中(设木板足够长,木块没脱离木板),则关于木板与地面之间的摩擦力大小的说法正确的是( )
如图所示,水平恒力F拉着质量为m的木块在水平放置在地面上的长木板上向右匀速运动,木板恰好能保持静止.则在此基础上,再逐渐增大F的过程中(设木板足够长,木块没脱离木板),则关于木板与地面之间的摩擦力大小的说法正确的是( )| A. | 恒为开始的F | |
| B. | 随F的增大而增大 | |
| C. | 由于木板没有运动,所以没有摩擦力 | |
| D. | 由于木板和地面的粗糙程度不知道,所以无法判断 |
| A. | 物体的温度越高,分子热运动越剧烈,分子平均动能越大,且每一个分子的动能越大 | |
| B. | 布朗运动就是液体分子的热运动 | |
| C. | 一切达到热平衡的系统一定具有相同的内能 | |
| D. | 分子间的距离r存在某一值r0,当r<r0时,斥力大于引力,当r>r0时,引力大于斥力 |
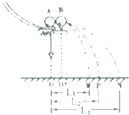 如图所示是已经调整好的探究动量守恒定律的装置,A、B是直径为d,质量分别为m1和m2的两个小球,且m1>m2.
如图所示是已经调整好的探究动量守恒定律的装置,A、B是直径为d,质量分别为m1和m2的两个小球,且m1>m2.