题目内容
【题目】物块A、B由跨过定滑轮的轻绳相连,A置于倾角θ=37°铺有动物皮毛的固定斜面上(物体在有动物皮毛的斜面上运动,由于皮毛的特殊性,引起物体的运动有如下特点,①顺着毛的生长方向运动时,毛皮产生的阻力可以忽略,②逆着毛的生长方向运动时,会受到来自毛皮的滑动摩擦力,且动摩擦因数恒定μ1=0.5,从物块A初始位置沿斜面向上铺有一段长L=4.5m的顺毛皮,后一段铺的都是逆毛皮。),B位于水平传送带的右端,轻绳分别与斜面、传送带平行,传送带始终以速度v0=3 m/s逆时针转动,如图所示。若将B轻放到传送带右端,A、B均处于平衡状态且A所受摩擦力为零。已知A的质量mA=1 kg,B与传送带间的动摩擦因数μ2=0.2,斜面、轻绳、传送带均足够长。物块A、B可视为质点,A不会碰到定滑轮,定滑轮的质量与摩擦力均不计。(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)

求:(1)物块B的质量mB?
(2)若某时刻B从传送带右端以速度v1=6 m/s向左运动,此时物块B的加速度大小?
(3)在上述(2)情况下,当物块B恰好运动到最左侧时,运动的总时间及在传送带上留下的滑痕长度?
【答案】(1)3kg (2)3m/s2 (3)4s 4.5m
【解析】
A、B均处于平衡状态,根据平衡条件可得B的质量;B向左运动的过程中分别以A与B为研究的对象,结合牛顿第二定律先求出B的加速度;应用牛顿第二定律求出在顺毛上的加速度,进而求出共速时间和相应的物块和传送带的位移,在应用牛顿第二定律求出在顺毛上的加速度,进而求出共速时间和相应的物块和传送带的位移,从而求出运动时间和划痕的长度。
(1)对A、B,根据平衡条件可得:![]()
代入数据解得:![]()
(2)B向左运动减速运动的过程中,刚开始时,B的速度大于传送带的速度,以B为研究的对象,水平方向B受到向右的摩擦力与A对B的拉力,设AB之间绳子的拉力为T1,以向右为正方向,得:T1+μ2mBg=mBa1
以A为研究的对象,则A的加速度的大小始终与B是相等的,A向上运动的过程中受力如图,

则:mAgsin37°- T1=mAa1
联立并代入数据解得:a1=3m/s2
(3)B的速度与传送带的速度相等时所用的时间为:![]() ,
,
运动的位移为:![]()
传送带的位移为:![]()
此时,在传送带上留下的滑痕长度![]()
当B的速度与传送带的速度相等之后,B仍然做减速运动,而此时B的速度小于传送带的速度,所以受到的摩擦力变成了向左,所以其加速度也发生了变化,此后B向左运动减速运动的过程中,设AB之间绳子的拉力为T2,以B为研究的对象,水平方向B受到向左的摩擦力与A对B的拉力,则:μ2mBg-T2=mBa2
以A为研究的对象,则A的加速度的大小始终与B是相等的,A向上运动的过程中受力如图,则:T2-mAgsin37°-μ1mAgcos37°=mAa2
联立并代入数据解得:a2=1m/s2
由上可知A进入逆毛区后速度为3m/s,接下来将一直减速到零,
根据速度时间公式可得: ![]()
运动的位移为:![]()
传送带的位移为:![]()
所以当物块B恰好运动到最左侧时,运动的总时间为:![]()
传送带上留下的滑痕长度:![]()
因为后面的滑痕会覆盖了前面的滑痕,所以当物块B恰好运动到最左侧时在传送带上留下的滑痕长度是![]()

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】在厦门集美双龙潭里有一种滑草游乐活动。如图所示,人坐在滑板上从斜坡的高处A点由静止开始滑下,经过B点后进入水平的滑道(设经过B点前后速度大小不变),最后停在C点。若此人和滑板的总质量m=60 kg,每隔1s通过速度测量仪器测量人的瞬时速度大小,测量数据如下表所示。假设滑板与斜坡滑道和水平滑道间的动摩擦因数相同,整个运动过程中空气阻力不计。(g取10 m/s2,sin 15°=0.26,sin25°=0.42,sin 37°=0.60,sin40°=0.64,sin 50°=0.76)
时刻t/s | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
速度v/(m·s-1) | 0 | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 | 12.0 | 12.6 | 7.6 | 2.6 | 0 |
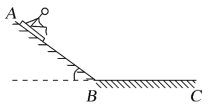
求:(1)物体与滑道之间的动摩擦因数μ?
(2)斜坡滑道的倾角θ?
(3)斜坡滑道受到人和滑板所施加作用力F的大小?