题目内容
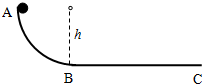
A如图所示，质量为2千克的物体，在竖直平面内高h=0.8米的光滑弧形轨道A点，由静止起沿轨道滑下，并进入BC轨道．已知BC段的动摩擦因数?=0.4，求（1）物体滑至B点时的速度；
（2）物体最后静止处距B点的距离．
分析：（1）物体从A滑到B点过程中，应用动能定理可以求出物体在B点的速度．
（2）根据牛顿第二定律求出加速度，再根据运动学公式求解．
（2）根据牛顿第二定律求出加速度，再根据运动学公式求解．
解答：解：（1）物体在AB轨道运动时运用动能定理得：
mgh=
mvB2
解得v=
=4（m/s）
（2）由-μ mg=ma得：
a=-μ g=-0.4×10=-4（m/s2）
则s=
=2（m）
答：（1）物体滑至B点时的速度为4m/s；
（2）物体最后静止处距B点的距离为2m．
mgh=
| 1 |
| 2 |
解得v=
| 2gh |
（2）由-μ mg=ma得：
a=-μ g=-0.4×10=-4（m/s2）
则s=
| 0-vB2 |
| 2a |
答：（1）物体滑至B点时的速度为4m/s；
（2）物体最后静止处距B点的距离为2m．
点评：熟练应用动能定理即可正确解题，本题难度不大；本题最后一问也可以应用动能定理解题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
如图所示，质量为2.0kg的木块放在水平桌面上的A点，受到一冲量后以某一速度在桌面上沿直线向右运动，运动到桌边B点后水平滑出落在水平地面C点．已知木块与桌面间的动摩擦因数为0.20，桌面距离水平地面的高度为1.25m，A、B两点的距离为4.0m，B、C两点间的水平距离为1.5m，g=10m/s2．不计空气阻力，求：
如图所示，质量为2.0kg的木块放在水平桌面上的A点，受到一冲量后以某一速度在桌面上沿直线向右运动，运动到桌边B点后水平滑出落在水平地面C点．已知木块与桌面间的动摩擦因数为0.20，桌面距离水平地面的高度为1.25m，A、B两点的距离为4.0m，B、C两点间的水平距离为1.5m，g=10m/s2．不计空气阻力，求：
