题目内容
【题目】如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于 ![]() ,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )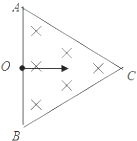
A.Bmin= ![]() ,t=
,t= ![]()
B.Bmin= ![]() ,t=
,t= ![]()
C.Bmin= ![]() ,t=
,t= ![]()
D.Bmin= ![]() ,t=
,t= ![]()
【答案】C
【解析】解:粒子在磁场中做圆周运动的半径为r,则 ![]() ,得
,得 ![]() ,因粒子从O孔水平射入后,最终又要水平射出,则有
,因粒子从O孔水平射入后,最终又要水平射出,则有 ![]() ,(n=1、2、3…),联立得
,(n=1、2、3…),联立得 ![]() ,当n=1时B取最小值,
,当n=1时B取最小值, ![]() ,此时对应粒子的运动时间为
,此时对应粒子的运动时间为 ![]() ,而
,而 ![]() ,
, ![]() ,C正确,ABD错误.
,C正确,ABD错误.
故选:C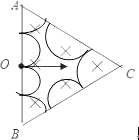
【考点精析】掌握向心力和洛伦兹力是解答本题的根本,需要知道向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力;洛伦兹力始终垂直于v的方向,所以洛伦兹力一定不做功.

练习册系列答案
相关题目