题目内容
 如图所示,一个带电荷量为+Q的点电荷甲固定在绝缘水平面上的O点,另一个带电荷量为-q,质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲滑行运动,运动到B点静止,已知静电力常量为K,点电荷乙与水平面的动摩擦因数为μ.A,B间的距离为S,下列说法正确的是( )
如图所示,一个带电荷量为+Q的点电荷甲固定在绝缘水平面上的O点,另一个带电荷量为-q,质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲滑行运动,运动到B点静止,已知静电力常量为K,点电荷乙与水平面的动摩擦因数为μ.A,B间的距离为S,下列说法正确的是( )分析:本题首先要正确分析物体受力特点,明确力和运动的关系,在本题中注意滑动摩擦力的大小方向不变,两球靠近过程中库仑力逐渐增大,小球先减速后加速,根据牛顿第二定律和功能关系可正确解答.
解答:解:A、从A点以初速度v0沿它们的连线向甲滑行运动,运动到B点静止,处于平衡状态,若最大静摩擦力等于滑动摩擦力,则有:mgμ=F库=k
,解得:r=
,故A错误;
B、在小球向左运动过程中,若做匀减速运动,因此中间时刻的速度等于
,如今做加速度减小的减速运动,所以中间时刻的速度小于
,如图所示;故B正确;
C、从A到B的过程中,电场力对点电荷乙做正功,导致电势能减小,因此产生的内能大于
mv02,故C错误.
D、点电荷从A运动B过程中,根据动能定理有:UABq-mgμL0=
mv2-
m
,解得,UAB=
.故D正确.
故选BD
| r2 |
|
B、在小球向左运动过程中,若做匀减速运动,因此中间时刻的速度等于
| v0 |
| 2 |
| v0 |
| 2 |

C、从A到B的过程中,电场力对点电荷乙做正功,导致电势能减小,因此产生的内能大于
| 1 |
| 2 |
D、点电荷从A运动B过程中,根据动能定理有:UABq-mgμL0=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
m(
| ||
| 2q |
故选BD
点评:本题在借助库仑力的基础知识,考查了力与运动、牛顿第二定理、动能定理等基础知识的综合应用,是考查学生综合能力的好题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
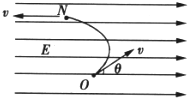 如图所示,一个带电荷量为-q的油滴,从O点以速度v射入匀强电场中,v的方向与电场方向成θ角.已知油滴的质量为m,测得油滴到达运动轨迹的最高点N时,它的速度大小仍为v.求:
如图所示,一个带电荷量为-q的油滴,从O点以速度v射入匀强电场中,v的方向与电场方向成θ角.已知油滴的质量为m,测得油滴到达运动轨迹的最高点N时,它的速度大小仍为v.求: Q,q对原电场无影响)可看做点电荷的小球,从B点无初速释放,如果小球质量为m,下滑过程中带电荷量不变,求:
Q,q对原电场无影响)可看做点电荷的小球,从B点无初速释放,如果小球质量为m,下滑过程中带电荷量不变,求:






