Question

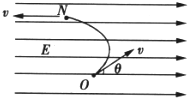如图所示，一个带电荷量为-q的油滴，从O点以速度v射入匀强电场中，v的方向与电场方向成θ角．已知油滴的质量为m，测得油滴到达运动轨迹的最高点N时，它的速度大小仍为v．求：
（1）最高点与O点的竖直高度；
（2）最高点与O点的电势差U_NO；
（3）电场强度E．

Answer 1

分析：（1）由题，油滴从O到N的过程，竖直方向上做竖直上抛运动，由运动学公式求解竖直高度h；
（2）油滴从O到N的过程，动能不变，重力做负功-mgh，根据动能定理求解电势差U_NO；
（3）采用运动的分解法，分别由运动学速度公式得到竖直和水平两个方向的速度与时间的关系式，抓住时间相等，即可求出加速度，由牛顿第二定律求得场强E．

解答：解：（1）在竖直方向上，液滴做竖直上抛运动，则有
  （vsinθ）²=2gh
解得 h=

v2sin2θ

2g

（2）油滴从O到N的过程，由动能定理得：U_NOq-mgh=0
解得 U_NO=

mv2sin2θ

2q

（3）竖直方向上：vsinθ=gt
设水平方向的加速度大小为a，则
-v=vcosθ-at
又 Eq=ma
联立以上三式得：E=

mgsinθ

q(1-cosθ)

答：
（1）最高点与O点的竖直高度是

v2sin2θ

2g

；
（2）最高点与O点的电势差U_NO是

mv2sin2θ

2q

．
（3）电场强度E是

mgsinθ

q(1-cosθ)

．

点评：本题采用运动的分解法研究一般的曲线运动，抓住两个分运动的等时性，由运动学公式、动能定理和牛顿第二定律结合进行求解．