题目内容
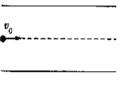
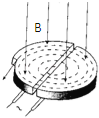
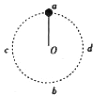
【题目】如图甲所示,竖直平面内正方形线框IJKT通过极小的开口PQ用导线与电阻器R、平行金属板AB相连,PIJKTQ间的电阻值与电阻器R的阻值相等,AB板上下间距d=20m。在正方形线框内有一圆形匀强磁场区,面积S=10m2,磁感强度的方向垂直向里、大小为Bt(Bt为磁感强度B随时间t变化的函数)。t=0s时刻在AB板的中间位置P静止释放一个质量为m=1kg、电量为q=+1C的小球(可视为质点)。已知重力加速度g=10m/s2;不计变化磁场在PQ右侧产生的电动势;不计导线的电阻。
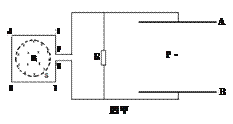

⑴如果Bt=bt(T)(t≥0s),b为定值。静止释放小球后,小球一直处于静止,求b值。
⑵如果0s≤t≤1s:Bt=56t(T);t>1s:Bt=0(T)。静止释放小球后,经多长时间小球落到B板上。
⑶如果Bt按如图乙所示的方式变化(已知各段图像相互平行,第一段图像的最高点的坐标为:(1s、80T)。静止释放小球后,小球向上或向下运动过程中加速度方向只变化1次,且小球恰好不与A、B板碰撞。求图乙中的Bm和tn。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
![]()
【解析】(1)感应电动势为E1:E1=![]() S,
S,
电容器两端的电压为U1:U1=![]()
小球电场力等于重力:q![]() =mg,
=mg,
综上,解得:b=40T/s;
(2)①0≤t≤1s时,感应电动势为E2:E2=![]() S,U2=
S,U2=![]() E2;
E2;
小球加速度a1,根据牛顿第二定律,有:q![]() mg=ma1,
mg=ma1,
解得:a1=4m/s2;
在1s内的位移为x1=![]() a1t22,x1=2m<
a1t22,x1=2m<![]() ;
;
在1s末的速度为:v1=a1t1=4m/s;
②t>1s时:感应电动势为0,小球的加速度为a2=g;
运动时间为t2,根据位移公式,有: ![]() d+x1=v1t2
d+x1=v1t2![]() a2 t22
a2 t22
解得:t2=2s;
③t总=t1+t2=3s;
(3)①0-1s内:小球加速度:a=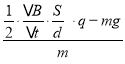 =10m/s2=g;
=10m/s2=g;
②根据对称性,第1次向上加速、减速所经历时间都为△t,根据位移公式,有:5m=![]() a△t2,解得:△t=1s;
a△t2,解得:△t=1s;
③根据对称性,第2、3、…、n次向上和向下加速、减速所经历时间:10m=![]() a△t12,解得:△t1=
a△t12,解得:△t1=![]() s;
s;
④Bm=2![]() △t1=160
△t1=160![]() (T);
(T);
⑤tn=4![]() n+(2
n+(2![]() ),(n=1、2、3…);
),(n=1、2、3…);

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案