题目内容
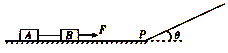
【题目】如图所示，足够长的倾角θ=37°的斜面与水平地面在P点平滑连接，通过轻绳连接的A、B两物体静置于水平地面上，质量分别为m1=2kg，m2=4kg，此时轻绳处于水平且无拉力，物体A与接触面之间的动摩擦因数均为μ1=0.5，物体B与 接触面之间的动摩擦因数均为μ2=0.75。对物体B施加水平恒力F=76N，使两物体一起向右加速运动，经过时间t=2s物体B到达斜面底端P点，此时撤去恒力F。若两物体均可视为质点，重力加速度g=10m/s2， （物块在P点无机械能损失）求：
（1）请计算两物体加速时轻绳上的力T；
（2）进入斜面后，两物体恰好不相撞，求轻绳的长度L。
【答案】（1）22N （2）2.4m
【解析】（1）两物体加速时对整体研究有：
F-μ1m1g-μ2m2g=（m1+m2）a
对A物体有：T-μ1m1g=m1a
两式联立可得：T=22N，a=6m/s2
（2）物体B到达斜面底端的速度为：v=at=12m/s
物体B到到斜面后，做减速运动，根据牛顿第二定律可知：
物体B在斜面上上滑的位移为：
设AB间的绳长为L，则A在水平面上的加速度为：
＝5m/s2，到达斜面底端的速度为v′，则有：v′2-v2=2a′L
A在斜面上的加速度为：
，在斜面上运动的有运动学公式可知：
联立解得：L=2.4m
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
