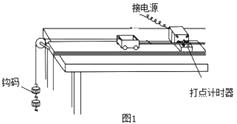
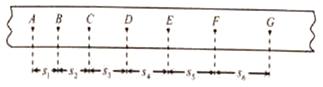
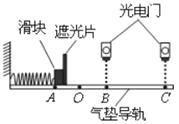
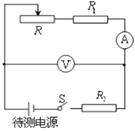
题目内容
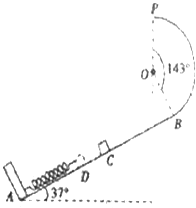
【题目】如图所示，图面内有竖直线DD＇，过DD＇且垂直于图面的平面将空间分成I、II两区域。区域I有方向竖直向上的匀强电场和方向垂直图面的匀强磁场B（图中未画出）；区域II有固定在水平面上高 h=2l 、倾角 
的光滑绝缘斜面，斜面顶端与直线DD＇距离 s=4l ，区域II可加竖直方向的大小不同的匀强电场（图中未画出）；C点在DD＇上，距地面高 H=3l 。零时刻，质量为m、带电荷量为q的小球P在K点具有大小 
、方向与水平面夹角 
的速度，在区域I内做半径 
的匀速圆周运动，经C点水平进入区域II。某时刻，不带电的绝缘小球A由斜面顶端静止释放，在某处与刚运动到斜面的小球P相遇。小球视为质点，不计空气阻力及小球P所带电量对空间电磁场的影响。l已知，g为重力加速度。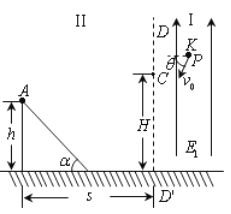 
（1）求匀强磁场的磁感应强度的大小；
（2）若小球A、P在斜面底端相遇，求释放小球A的时刻tA；
（3）若小球A、P在时刻 
（β为常数）相遇于斜面某处，求此情况下区域II的匀强电场的场强E，并讨论场强E的极大值和极小值及相应的方向。
【答案】
（1）
解：由题知，小球P在区域Ⅰ内做匀速圆周运动，有
①
代入数据解得 
②
答：匀强磁场的磁感应强度的大小为 。
（2）
解：小球P在区域Ⅰ做匀速圆周运动转过的圆心角为θ，运动到C点的时刻为tC，到达斜面低端时刻为t1，有 
③
④
小球A释放后沿斜面运动加速度为aA，与小球P在时刻t1相遇于斜面底端，有
⑤
⑥
联立以上方程可得 
⑦
答：释放小球A的时刻tA为 。
（3）
解：设所求电场方向向下，在t'A时刻释放小球A，小球P在区域Ⅱ运动加速度为aP，有
⑧
⑨
⑩
联立相关方程解得 
对小球P的所有运动情形讨论可得 
由此可得场强极小值为 
；场强极大值为 
，方向竖直向上
答：场强极小值为 ；场强极大值为 ，方向竖直向上。
【解析】（1）带电粒子在复合场中做匀速圆周运动，洛伦兹力提供向心力，电场力和重力平衡（2）求出小球A沿斜面匀加速运动的时间、小球P匀速圆周运动的时间及离开磁场类平抛运动的时间，根据时间关系求释放小球A的时刻（3）小球P进入Ⅱ区做类平抛运动，根据类平抛规律列式，结合数学知识求E的最值．
【考点精析】关于本题考查的平抛运动，需要了解特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动才能得出正确答案．
