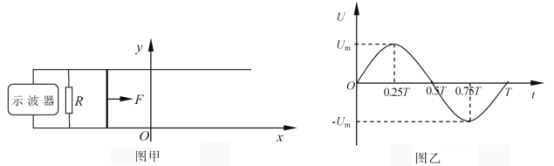
题目内容
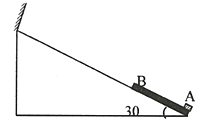
【题目】倾角为30°的粗糖斜面上端固定一个弹性挡板,质量m=lkg的小木块A放置于质量M=5kg的长木板B的下边缘,并且长木板的下边缘与斜面底端对齐,A、B—起以v0= 5m/s的初速度 从斜面底端向上冲,经过0.4s时间B与挡板发生碰撞(碰撞时间极短),速度大小不变方向相反, 已知小木块A与长木板B之间滑动摩擦系数μ1=![]() ,长木板B与斜面间的滑动摩擦系数μ2=
,长木板B与斜面间的滑动摩擦系数μ2=![]() ,取g=10m/s2,求
,取g=10m/s2,求
(1)长木板B与挡板碰后的速度大小
(2)若小木块A恰好不脱离长木板B,则B的下边缘刚好回到斜面底端时的速度大小是多少?
(3)在(2)问中,从B与挡板碰撞到B再次回到出发点所用的时间是多少?
【答案】(1) lm/s (2) ![]() m/s (3)
m/s (3) ![]() s
s
【解析】
(1)选AB整体为研究对象,从出发到B与挡板相碰过程中.时间t1=0.4s
(m +M)gsin30°+μ(m+M)gcos30°=(m+M)a
v1= v0-at1.
联立可解
v1=1m/s
B与挡板碰后速度大小不变为lm/s.
(2)B与挡板碰后,A与B组成的系统沿斜面方向合外力为零
(M+m)gsin30°=μ(M+m)gcos30°
所以AB系统沿斜面方向动量守恒,又由于A与B不脱离,因此二者恰好不脱离时必共速,设共速速度为v2,选沿斜面向下为正方向,
Mv1-mv1=(M+m)v2.
可得
v2=![]() m/s
m/s
即为B到达斜面底端速度。
(3)设B上端到斜面长为L,
L=![]() =1.2m.
=1.2m.
B与挡板碰后加速度为:
aB=![]() =-2.5m/s2
=-2.5m/s2
可知B与挡板碰后沿斜而向下做匀减速直线运动到与A共速,此过程经历时间设为△t1,
△t1=![]() s
s
设此过程前进位移x1,
x1=![]() m
m
B与A达到共速后.一起匀速走完剩余的长度,设此过程经历时间△t2,
△t2=![]() s
s
所以从B与挡板碰后到B再次回到出发点总时间为
△t=△t1+△t2=![]() s.
s.