Question

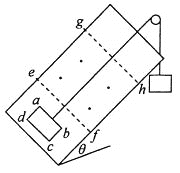
【题目】静止在水平地面上的两小物块A、B，质量分别为mA=l.0kg，mB=4.0kg；两者之间有一被压缩的微型弹簧，A与其右侧的竖直墙壁距离l=1.0m，如图所示。某时刻，将压缩的微型弹簧释放，使A、B瞬间分离，两物块获得的动能之和为Ek=10.0J。释放后，A沿着与墙壁垂直的方向向右运动。A、B与地面之间的动摩擦因数均为u=0.20。重力加速度取g=10m/s。A、B运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短。

（1）求弹簧释放后瞬间A、B速度的大小；

（2）物块A、B中的哪一个先停止？该物块刚停止时A与B之间的距离是多少？

（3）A和B都停止后，A与B之间的距离是多少？

Answer 1

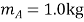
【答案】（1）vA=4.0m/s，vB=1.0m/s；（2）A先停止； 0.50m；（3）0.91m；

【解析】

首先需要理解弹簧释放后瞬间的过程内A、B组成的系统动量守恒，再结合能量关系求解出A、B各自的速度大小；很容易判定A、B都会做匀减速直线运动，并且易知是B先停下，至于A是否已经到达墙处，则需要根据计算确定，结合几何关系可算出第二问结果；再判断A向左运动停下来之前是否与B发生碰撞，也需要通过计算确定，结合空间关系，列式求解即可。

（1）设弹簧释放瞬间A和B的速度大小分别为vA、vB，以向右为正，由动量守恒定律和题给条件有

0=mAvA-mBvB①

②

联立①②式并代入题给数据得

vA=4.0m/s，vB=1.0m/s

（2）A、B两物块与地面间的动摩擦因数相等，因而两者滑动时加速度大小相等，设为a。假设A和B发生碰撞前，已经有一个物块停止，此物块应为弹簧释放后速度较小的B。设从弹簧释放到B停止所需时间为t，B向左运动的路程为sB。，则有

④

⑤

⑥

在时间t内，A可能与墙发生弹性碰撞，碰撞后A将向左运动，碰撞并不改变A的速度大小，所以无论此碰撞是否发生，A在时间t内的路程SA都可表示为

sA=vAt–⑦

联立③④⑤⑥⑦式并代入题给数据得

sA=1.75m，sB=0.25m⑧

这表明在时间t内A已与墙壁发生碰撞，但没有与B发生碰撞，此时A位于出发点右边0.25m处。B位于出发点左边0.25m处，两物块之间的距离s为

s=0.25m+0.25m=0.50m⑨

（3）t时刻后A将继续向左运动，假设它能与静止的B碰撞，碰撞时速度的大小为vA′，由动能定理有

⑩

联立③⑧⑩式并代入题给数据得

故A与B将发生碰撞。设碰撞后A、B的速度分别为vA′′以和vB′′，由动量守恒定律与机械能守恒定律有

联立式并代入题给数据得

这表明碰撞后A将向右运动，继续向左运动。设碰撞后A向右运动距离为sA′时停止，B向左运动距离为sB′时停止，由运动学公式

由④式及题给数据得

sA′小于碰撞处到墙壁的距离。由上式可得两物块停止后的距离