题目内容
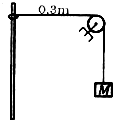 如图所示,轻绳一端挂一质量为M的物体,另一端系在质量为m的圆环上,圆环套在竖直固定的细杆上,定滑轮与细杆相距0.3m,将环拉至与滑轮在同一高度上,再将环由静止释放.圆环沿杆向下滑动的最大位移为0.4m,若不计一切摩擦阻力,求:
如图所示,轻绳一端挂一质量为M的物体,另一端系在质量为m的圆环上,圆环套在竖直固定的细杆上,定滑轮与细杆相距0.3m,将环拉至与滑轮在同一高度上,再将环由静止释放.圆环沿杆向下滑动的最大位移为0.4m,若不计一切摩擦阻力,求:(1)物体与环的质量比;
(2)圆环下落0.3m时速度大小.
分析:(1)根据几何关系及机械能守恒定律即可解题;
(2)可根据几何关系求出物体上升高度,由运动合成分解求出物体的速度,再根据机械能守恒即可解题.
(2)可根据几何关系求出物体上升高度,由运动合成分解求出物体的速度,再根据机械能守恒即可解题.
解答:解:(1)当环下降至最大位移处时,vm=vM=0
而此时物体上升的高度为h2=
-0.3=0.2m
由机械能守恒mgh1-
m
=Mgh2+
M
.得
=
(2)当圆环下降h1=0.30m时,物体上升高度为h2
h2=
-0.3=0.3(
-1)m
由运动合成分解得:vM=vmcos45°=
vm
由系统机械能守恒有mgh1-
m
=mgh2+
M
联立得圆环下落0.3米时速度大小:vm=0.72m/s
答:(1)物体与环的质量比为2:1;
(2)圆环下落0.3m时速度大小为0.72m/s.
而此时物体上升的高度为h2=
| 0.42+0.32 |
由机械能守恒mgh1-
| 1 |
| 2 |
| v | 2 m |
| 1 |
| 2 |
| v | 2 M |
| M |
| m |
| 2 |
| 1 |
(2)当圆环下降h1=0.30m时,物体上升高度为h2
h2=
| 0.32+0.32 |
| 2 |
由运动合成分解得:vM=vmcos45°=
| ||
| 2 |
由系统机械能守恒有mgh1-
| 1 |
| 2 |
| v | 2 m |
| 1 |
| 2 |
| v | 2 M |
联立得圆环下落0.3米时速度大小:vm=0.72m/s
答:(1)物体与环的质量比为2:1;
(2)圆环下落0.3m时速度大小为0.72m/s.
点评:该题主要考查了连接体问题的速度、位移关系,可以通过几何关系及机械能守恒定律去求解,难度适中.

练习册系列答案
相关题目
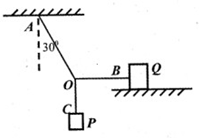 如图所示,轻绳OA一端系于天花板上,与竖直方向的夹角为30°,水平轻绳OB的一端系在一物体Q上,Q相对于水平桌面静止,OC绳挂一重为300N的物体P.试求绳子OA的拉力与物体Q受到的摩擦力的大小.
如图所示,轻绳OA一端系于天花板上,与竖直方向的夹角为30°,水平轻绳OB的一端系在一物体Q上,Q相对于水平桌面静止,OC绳挂一重为300N的物体P.试求绳子OA的拉力与物体Q受到的摩擦力的大小. 如图所示,轻绳OA一端系于天花板上,与竖直方向的夹角为30°,水平轻绳OB的一端系于竖直墙上,O点挂一重物.重物重力300N,此时绳OA、OB的拉力是多大?(结果保留三位有效数字)
如图所示,轻绳OA一端系于天花板上,与竖直方向的夹角为30°,水平轻绳OB的一端系于竖直墙上,O点挂一重物.重物重力300N,此时绳OA、OB的拉力是多大?(结果保留三位有效数字)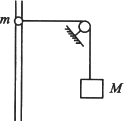
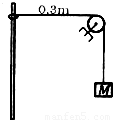 如图所示,轻绳一端挂一质量为M的物体,另一端系在质量为m的圆环上,圆环套在竖直固定的细杆上,定滑轮与细杆相距0.3m,将环拉至与滑轮在同一高度上,再将环由静止释放.圆环沿杆向下滑动的最大位移为0.4m,若不计一切摩擦阻力,求:
如图所示,轻绳一端挂一质量为M的物体,另一端系在质量为m的圆环上,圆环套在竖直固定的细杆上,定滑轮与细杆相距0.3m,将环拉至与滑轮在同一高度上,再将环由静止释放.圆环沿杆向下滑动的最大位移为0.4m,若不计一切摩擦阻力,求: