题目内容
12.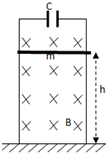 如图所示,间距为L的金属导轨竖直平行放置,空间有垂直于导轨所在平面向里、大小为B的匀强磁场.在导轨上端接一电容为C的电容器,一质量为m的金属棒ab与导轨始终保持良好接触,由静止开始释放,释放时ab 距地面高度为h,(重力加速度为g,一切摩擦及电阻均不计)在金属棒下滑至地面的过程中,下列说法正确的是( )
如图所示,间距为L的金属导轨竖直平行放置,空间有垂直于导轨所在平面向里、大小为B的匀强磁场.在导轨上端接一电容为C的电容器,一质量为m的金属棒ab与导轨始终保持良好接触,由静止开始释放,释放时ab 距地面高度为h,(重力加速度为g,一切摩擦及电阻均不计)在金属棒下滑至地面的过程中,下列说法正确的是( )| A. | 若h足够大,金属棒最终匀速下落 | |
| B. | 金属棒运动到地面时,电容器储存的电荷量为mgh | |
| C. | 金属棒做匀加速运动,加速度为$\frac{mg}{mg+{C}^{2}{B}^{2}{L}^{2}}$ | |
| D. | 金属棒运动到地面时,电容器储存的电势能为$\frac{mghC{B}^{2}{L}^{2}}{m+C{B}^{2}{L}^{2}}$ |
分析 由左手定则来确定安培力的方向,并求出安培力的大小;借助于I=$\frac{△Q}{△t}$、a=$\frac{△v}{△t}$及牛顿第二定律来求出加速度的表达式,分析金属棒的运动情况.金属棒的重力势能转化为金属棒的动能与电容器中的电势能.
解答 解:A、设金属棒的速度大小为v时,经历的时间为t,通过金属棒的电流为i,产生的电动势为:e=BLv
金属棒受到的安培力方向沿导轨向上,大小为:F=BLi
设在时间间隔(t,t+△t )内流经金属棒的电荷量为△Q,则△Q=C△U=C•△e
按电流的定义有:i=$\frac{△Q}{△t}$,△Q也是平行板电容器极板在时间间隔△t内增加的电荷量,
在△t内金属棒的速度变化量为△v,由加速度的定义有:a=$\frac{△v}{△t}$
金属棒在时刻t的加速度方向向下,设其大小为a,根据牛顿第二定律有:mg-F=ma
联立上此式可得:a=$\frac{mg}{m+C{B}^{2}{L}^{2}}$.则知加速度a为定值,金属棒做匀加速运动,且加速度为 $\frac{mg}{m+C{B}^{2}{L}^{2}}$.故A、C错误;
B、金属棒下降h后的速度为 v0=$\sqrt{2ah}$
电容器板间电压 U=BLv0=BL$\sqrt{2ah}$
电容器储存的电荷量为 Q=CU=CBL$\sqrt{2ah}$=CBL$\sqrt{\frac{2mgh}{m+C{B}^{2}{L}^{2}}}$,故B错误.
D、金属棒运动到地面时,金属棒的动能:EK=$\frac{1}{2}m{v}_{0}^{2}$=mah
金属棒的重力势能转化为金属棒的动能与电容器中的电势能,所以金属棒运动到地面时,电容器储存的电势能:
EP=mgh-EK=$\frac{mghC{B}^{2}{L}^{2}}{m+C{B}^{2}{L}^{2}}$.故D正确.
故选:D
点评 本题关键采用微元法分析金属棒的加速度,切入点是加速度的定义式,再应用牛顿第二定律、匀变速运动的速度公式、E=BLv即可正确解题.

| A. | 加速度是表示速度的物理量 | |
| B. | 加速度是表示速度变化的物理量 | |
| C. | 加速度是表示速度变化快慢的物理量 | |
| D. | 运动物体的加速度与速度没有联系 |
| A. | 位移与路程有时是相同的 | |
| B. | 位移描述直线运动,路程描述曲线运动 | |
| C. | 田径运动会上田赛项目测量的是位移的大小 | |
| D. | 出租车司机是按位移收费的 |

(1)设电火花计时器的周期为T,计算F点的瞬时速度vF的公式为vF=$\frac{{d}_{6}-{d}_{4}}{2T}$;
(2)若电火花计时器的周期为T=0.02s,各个间距的数值如下表,求出物体的加速度a=0.51 m/s2(结果保留两位有效数字);
| d1 | d2 | d3 | d4 | d5 | d6 | |
| 间距(cm) | 0.68 | 1.86 | 3.55 | 5.76 | 8.46 | 11.65 |
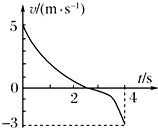
| A. | 4 s内物体在做曲线运动 | |
| B. | 4 s内物体的速度一直在减小 | |
| C. | 物体的加速度在2.5 s时方向改变 | |
| D. | 4 s内物体速度的变化量的大小为8 m/s |
 音圈电机是一种应用于硬盘、光驱等系统的特殊电动机.如图是某音圈电机的原理示意图,它由一对正对的磁极和一个正方形刚性线圈构成,线圈边长为L,匝数为n,磁极正对区域内的磁感应强度方向垂直于线圈平面竖直向下,大小为B,区域外的磁场忽略不计.线圈左边始终在磁场外,右边始终在磁场内,前后两边在磁场内的长度始终相等.某时刻线圈中电流从P流向Q,大小为I.求此时线圈所受安培力的大小和方向.
音圈电机是一种应用于硬盘、光驱等系统的特殊电动机.如图是某音圈电机的原理示意图,它由一对正对的磁极和一个正方形刚性线圈构成,线圈边长为L,匝数为n,磁极正对区域内的磁感应强度方向垂直于线圈平面竖直向下,大小为B,区域外的磁场忽略不计.线圈左边始终在磁场外,右边始终在磁场内,前后两边在磁场内的长度始终相等.某时刻线圈中电流从P流向Q,大小为I.求此时线圈所受安培力的大小和方向. 如图所示,变阻器R2的最大电阻是6Ω,与有关规格为(6V,3W)的灯泡R1串联接在电路中,电源的电动势E=8V,当电键S闭合,变阻器的滑片在中点位置时,灯泡正常发光,设灯泡阻值恒定不变,求:
如图所示,变阻器R2的最大电阻是6Ω,与有关规格为(6V,3W)的灯泡R1串联接在电路中,电源的电动势E=8V,当电键S闭合,变阻器的滑片在中点位置时,灯泡正常发光,设灯泡阻值恒定不变,求: 如图所示,MN为一竖直放置足够大的荧光屏,距荧光屏左边l的空间存在着一宽度也为l、方向垂直纸面向里的水平匀强磁场,O为荧光屏上的一点,OO′与荧光屏垂直,一质量为m、电荷量为q的带正电的粒子(重力不计)以初速度v0从O点沿OO′方向射入磁场区域.粒子离开磁场后打到荧光屏上时,速度方向与竖直方向成30°角.
如图所示,MN为一竖直放置足够大的荧光屏,距荧光屏左边l的空间存在着一宽度也为l、方向垂直纸面向里的水平匀强磁场,O为荧光屏上的一点,OO′与荧光屏垂直,一质量为m、电荷量为q的带正电的粒子(重力不计)以初速度v0从O点沿OO′方向射入磁场区域.粒子离开磁场后打到荧光屏上时,速度方向与竖直方向成30°角.