��Ŀ����
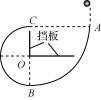
����Ŀ����ͼ��ʾ����ֱƽ���ڵĹ⻬�̶�������ķ�֮һԲ��AB�Ͷ���֮һԲ��BC�������������͵�B��ƽ������. ��BCԲ����Բ��O�к�Ȳ��Ƶ�ˮƽ�������ֱ�����һ����������Բ�����֮���п��Ⱥ�С�ķ�϶. AB���İ뾶Ϊ2R��BC���İ뾶ΪR. һ��ֱ����С�ڷ��������Ϊm��С����A�����Ϸ�![]() R���ɾ�ֹ��ʼ������������A����Բ������˶���������С��ײ�������Ժ����������ٶ�Ϊg.��
R���ɾ�ֹ��ʼ������������A����Բ������˶���������С��ײ�������Ժ����������ٶ�Ϊg.��
 ��
��
(1) С���������䵽A��ʱ���ٶȴ�С��
(2) С��C��ʱ����������ĵ�����С��
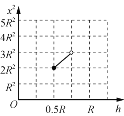
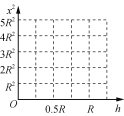
(3) С���A��h���������½���������C���׳�����ˮƽ�����ϵ���㵽O��ľ���x��h�仯�Ĺ�ϵʽ������ͼ�л���x2-hͼ����
���𰸡���1��![]() ��2��
��2��![]() mg��3��ͼ����ͼ��ʾ��
mg��3��ͼ����ͼ��ʾ��
��������
��1�����ݶ��ܶ������С���������䵽A��ʱ���ٶȣ���2������ţ�ٵڶ������������С��ĵ�������3��С���������£���ABCԲ���������C�����ƽ���˶�������ƽ���˶��Ĺ������h�ķ�Χ������ͼ��
(1) �ɶ��ܶ�����֪��![]()
vA��2![]() .
.
(2) ������С��ĵ���ΪF������ţ�ٵڶ����ɵ�
F��mg��m![]()
vC��vA��2![]()
�����F��![]() mg.
mg.
(3) С���������£���ABCԲ���������C�����ƽ���˶���
mgh��![]() mvC2
mvC2
R��![]() gt2
gt2
x��vCt
x��2![]()
��Ϊx<![]() R����vC��
R����vC��![]()
����![]() ��h<
��h<![]() R
R
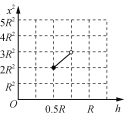
x2-hͼ����ͼ��ʾ��