题目内容
(1)用如图所示的实验装置验证牛顿第二定律.
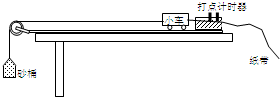
①完成平衡摩擦力的相关内容:
(i)取下砂桶,把木板不带滑轮的一端垫高,接通打点计时器电源,
(ii)如果打出的纸带如图所示,则应

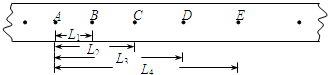
②如图所示是某次实验中得到的一条纸带,其中A、B、C、D、E是计数点(每打5个点取一个计数点),其中L1=3.07cm,L2=12.38cm,L3=27.87cm,L4=49.62cm.则打C点时小车的速度为
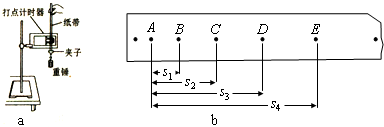
(2)用如图a所示的装置“验证机械能守恒定律”
①下列物理量需要测量的是
A.重锤质量 B.重力加速度
C.重锤下落的高度 D.与下落高度对应的重锤的瞬时速度
②设重锤质量为m、打点计时器的打点周期为T、重力加速度为g.图b是实验得到的一条纸带,A、B、C、D、E为相邻的连续点.根据测得的s1、s2、s3、s4写出重物由B点到D点势能减少量的表达式
.由于重锤下落时要克服阻力做功,所以该实验的动能增量总是

①完成平衡摩擦力的相关内容:
(i)取下砂桶,把木板不带滑轮的一端垫高,接通打点计时器电源,
轻推
轻推
(选填“静止释放”或“轻推”)小车,让小车拖着纸带运动.(ii)如果打出的纸带如图所示,则应
减小
减小
(选填“增大”或“减小”)木板的倾角,反复调节,直到纸带上打出的点迹间隔均匀
间隔均匀
,平衡摩擦力才完成.
②如图所示是某次实验中得到的一条纸带,其中A、B、C、D、E是计数点(每打5个点取一个计数点),其中L1=3.07cm,L2=12.38cm,L3=27.87cm,L4=49.62cm.则打C点时小车的速度为
1.24
1.24
m/s,小车的加速度是6.22
6.22
m/s2.(计算结果均保留三位有效数字)
(2)用如图a所示的装置“验证机械能守恒定律”
①下列物理量需要测量的是
C
C
、通过计算得到的是D
D
(填写代号)A.重锤质量 B.重力加速度
C.重锤下落的高度 D.与下落高度对应的重锤的瞬时速度
②设重锤质量为m、打点计时器的打点周期为T、重力加速度为g.图b是实验得到的一条纸带,A、B、C、D、E为相邻的连续点.根据测得的s1、s2、s3、s4写出重物由B点到D点势能减少量的表达式
(s3-s1)mg
(s3-s1)mg
,动能增量的表达式ms4(
| ||
| 8T2 |
ms4(
| ||
| 8T2 |
小于
小于
(填“大于”、“等于”或“小于”)重力势能的减小量.
分析:(1)平衡摩擦力时轻推小车,若小车能够做匀速直线运动,则摩擦力得到平衡.根据某段时间内的平均速度等于中间时刻的瞬时速度求出C点的速度,根据连续相等时间内的位移之差是一恒量求出小车的加速度.
(2)“验证机械能守恒定律”需验证重力势能的减小量与动能的增加量是否相等.
(2)“验证机械能守恒定律”需验证重力势能的减小量与动能的增加量是否相等.
解答:解:(1)①平衡摩擦力时,取下砂桶,把木板不带滑轮的一端垫高,接通打点计时器电源,若小车拖着纸带做匀速直线运动,则摩擦力得到平衡.
从纸带上看出,相等时间内位移越来越大,知小车做加速运动,需减小木板的倾角,直至小车做匀速直线运动,当纸带上打出的点迹间隔均匀,说明小车做匀速直线运动.
②小车通过C点的速度vc=
=
=
=1.24m/s.
a1=
,a2=
,所以a=
=
=6.22m/s2.
(2)①重锤的质量可测可不测,因为动能的增加量和重力势能的减小量式子中都有质量,可以约去.需要测量的物理量是C:重锤下落的高度,通过计算得到的物理量是D:与下落高度对应的重锤的瞬时速度.
②重物由B点到D点势能减少量的表达式为(s3-s1)mg,B点的速度vB=
,D点的速度vD=
,则动能的增加量△EK=
mvD2-
mvB2=
.
由于重锤下落时要克服阻力做功,有内能产生,根据能量守恒定律知,该实验的动能增量总是小于重力势能的减小量.
故答案为:(1)①(i)轻推(ii)减小,间隔均匀(之间的距离大致相等);
②1.24,6.22;
(2)①C、D ②(s3-s1)mg,
,小于
从纸带上看出,相等时间内位移越来越大,知小车做加速运动,需减小木板的倾角,直至小车做匀速直线运动,当纸带上打出的点迹间隔均匀,说明小车做匀速直线运动.
②小车通过C点的速度vc=
| xBD |
| 2T |
| L3-L1 |
| 2T |
| (27.87-3.07)×10-2 |
| 0.2 |
a1=
| xCD-xAB |
| 2T2 |
| xDE-xBC |
| 2T2 |
| a1+a2 |
| 2 |
| xCE-xAC |
| 4T2 |
(2)①重锤的质量可测可不测,因为动能的增加量和重力势能的减小量式子中都有质量,可以约去.需要测量的物理量是C:重锤下落的高度,通过计算得到的物理量是D:与下落高度对应的重锤的瞬时速度.
②重物由B点到D点势能减少量的表达式为(s3-s1)mg,B点的速度vB=
| s2 |
| 2T |
| s4-s2 |
| 2T |
| 1 |
| 2 |
| 1 |
| 2 |
ms4(
| ||
| 8T2 |
由于重锤下落时要克服阻力做功,有内能产生,根据能量守恒定律知,该实验的动能增量总是小于重力势能的减小量.
故答案为:(1)①(i)轻推(ii)减小,间隔均匀(之间的距离大致相等);
②1.24,6.22;
(2)①C、D ②(s3-s1)mg,
ms4(
| ||
| 8T2 |
点评:解决本题的关键掌握平衡摩擦力的方法,纸带的处理,以及掌握验证机械能守恒定律的原理.

练习册系列答案
相关题目
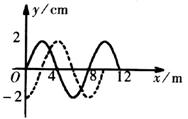
 一列简谐横波在 x 轴上传播,在 t1=0 和 t2=0.05s 时,其波形图分别用如图所示的实线和虚线表示,求:
一列简谐横波在 x 轴上传播,在 t1=0 和 t2=0.05s 时,其波形图分别用如图所示的实线和虚线表示,求: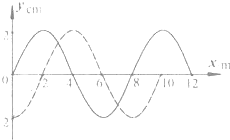 一列简谐横波在x轴上传播,在t1=0和t2=0.05s时刻,其波形图分别用如图所示的实线和虚线表示,求:
一列简谐横波在x轴上传播,在t1=0和t2=0.05s时刻,其波形图分别用如图所示的实线和虚线表示,求: