题目内容
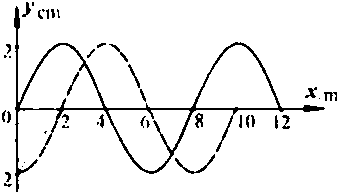
 一列简谐横波在 x 轴上传播,在 t1=0 和 t2=0.05s 时,其波形图分别用如图所示的实线和虚线表示,求:
一列简谐横波在 x 轴上传播,在 t1=0 和 t2=0.05s 时,其波形图分别用如图所示的实线和虚线表示,求:(1)这列波可能具有的波速
(2)当波速为 280m/s时,波的传播方向如何?此时图中质点 P 从图中位置运动至波谷所需的最短时间是多少.
分析:(1)由y的最大值读出振幅,由相邻两个波峰或波谷间的距离读出波长.根据波形的平移法,结合波的周期性,得出波传播的距离与波长的关系,求出波长的通项,再求解波速通项.
(2)当波速为280m/s时,求出△t=0.05s时间内波的传播距离,根据波形的平移法确定波传播方向,并根据周期来求出最短时间.
(2)当波速为280m/s时,求出△t=0.05s时间内波的传播距离,根据波形的平移法确定波传播方向,并根据周期来求出最短时间.
解答:解:(1)由对波形图分析可知,该波波长 λ=8 m.若波沿 x 轴正向传播,则有:
△x1=nλ+
=(8n+2)=v1△t (n=0、1、2、3 …)
∴v1=(8n+2)
=(8n+2)×
=(40+160 n) m/s
若波沿 x 轴负向传播,则有:
△x2=nλ+
=(8n+6)=v2△t (n=0、1、2、3 …)
∴v2=(8n+6)
=(8n+6)×
=(120+160 n) m/s
于是得到波速 v 的通式为:v=(40+80 k) m/s
当 k=0、2、4 …时,波沿x轴正向传播.
当 k=1、3、5 …时,波沿x轴负向传播.
(2)当波速为 280 m/s时,则有:280=40+80 k.
解得:k=3 故波沿-x 方向传播.
∵v=
∴T=
=
s=
s
P 质点第一次达到波谷的所历时间
t=
T=
×
=
=2.1×10-2 s
答:(1)这列波可能具有的波速v=(40+80 k) m/s
当 k=0、2、4 …时,波沿x轴正向传播.
当 k=1、3、5 …时,波沿x轴负向传播.
(2)当波速为 280m/s时,波沿-x 方向传播. 此时图中质点 P 从图中位置运动至波谷所需的最短时间是2.1×10-2 s.
△x1=nλ+
| λ |
| 4 |
∴v1=(8n+2)
| 1 |
| △t |
| 1 |
| 0.05 |
若波沿 x 轴负向传播,则有:
△x2=nλ+
| 3λ |
| 4 |
∴v2=(8n+6)
| 1 |
| △t |
| 1 |
| 0.05 |
于是得到波速 v 的通式为:v=(40+80 k) m/s
当 k=0、2、4 …时,波沿x轴正向传播.
当 k=1、3、5 …时,波沿x轴负向传播.
(2)当波速为 280 m/s时,则有:280=40+80 k.
解得:k=3 故波沿-x 方向传播.
∵v=
| λ |
| T |
∴T=
| v |
| 8 |
| 280 |
| 1 |
| 35 |
P 质点第一次达到波谷的所历时间
t=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 35 |
| 3 |
| 140 |
答:(1)这列波可能具有的波速v=(40+80 k) m/s
当 k=0、2、4 …时,波沿x轴正向传播.
当 k=1、3、5 …时,波沿x轴负向传播.
(2)当波速为 280m/s时,波沿-x 方向传播. 此时图中质点 P 从图中位置运动至波谷所需的最短时间是2.1×10-2 s.
点评:本题关键要抓住波的周期性和双向性,根据波形的平移法确定波传播距离与波长的关系.

练习册系列答案
相关题目

 一列简谐横波在x轴上传播,某时刻的波形图如图所示,a、b、c为简谐波中的三个质点,a正向下运动.下列判断正确的是( )
一列简谐横波在x轴上传播,某时刻的波形图如图所示,a、b、c为简谐波中的三个质点,a正向下运动.下列判断正确的是( )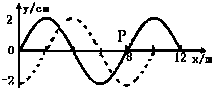 一列简谐横波在x轴上传播,在t1=0和t2=0.1s时刻,其波形图分别如图中的实线和虚线所示,求:
一列简谐横波在x轴上传播,在t1=0和t2=0.1s时刻,其波形图分别如图中的实线和虚线所示,求: