题目内容
 如图所示,支架的质量为M,转轴O处悬挂一个质量为m的小球,绳长为L,绳的质量可以忽略.若小球在竖直平面内做圆周运动,到达最高点时,恰好支架对地面无压力.则小球运动到最高点时的速度大小等于多少?
如图所示,支架的质量为M,转轴O处悬挂一个质量为m的小球,绳长为L,绳的质量可以忽略.若小球在竖直平面内做圆周运动,到达最高点时,恰好支架对地面无压力.则小球运动到最高点时的速度大小等于多少?分析:到达最高点时,恰好支架对地面无压力为零,则绳对支架的拉力为Mg,则绳对小球的作用力为Mg,合外力提供小球圆周运动的向心力,根据牛顿第二定律列式求解速度.
解答:解:设最高点绳子的拉力为F,小球速度为v,
以M为研究对象,支架对地面无压力为零,则F-Mg=0①
以m为研究对象得:F+mg=m
②
由①②解得:v=
答:小球运动到最高点时的速度大小等于
.
以M为研究对象,支架对地面无压力为零,则F-Mg=0①
以m为研究对象得:F+mg=m
| v2 |
| L |
由①②解得:v=
|
答:小球运动到最高点时的速度大小等于
|
点评:本题关键是根据向心力公式和牛顿第二定律公式列式求解,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
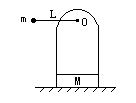
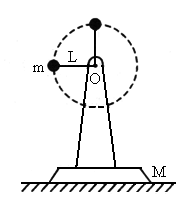

 如图所示,支架的质量为M,置于水平地面上,转轴O悬挂一个质量为m的小球,绳长为 L,将小球从图中水平位置以某一速度释放,为了使小球能绕O点在竖直平面内做圆周运动,且支架不至于离开地面,小球释放时初速度应满足什么条件?
如图所示,支架的质量为M,置于水平地面上,转轴O悬挂一个质量为m的小球,绳长为 L,将小球从图中水平位置以某一速度释放,为了使小球能绕O点在竖直平面内做圆周运动,且支架不至于离开地面,小球释放时初速度应满足什么条件?