题目内容
如图所示,竖直墙和3/4光滑圆轨道相切于A点,圆轨道的最低点为B、最高点为C、圆心为O、半径为R,小物体从紧贴墙的位置P由静止释放,欲使小物体不离开圆轨道,最终打在竖直墙上位置Q(图中未画出)处,并且QA距离最小,求PQ的距离.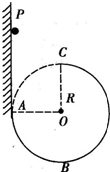

小物体离开C点做平抛运动,落在墙上的Q点,设经过C点的速度为v
水平方向:R=vt,竖直下落的高度为y=
gt2
则y=
.
由此可知经过C点的速度越大,下落高度越小,QA距离越大,所以通过C点的速度最小时,QA的距离最小,设小物体经过C点时的速度最小为v1.
根据牛顿第二定律有:
mg=
此时ymin=
=
R.
设PC高度差为h,因为小物体对竖直墙的压力为零,所以小物体受到墙的摩擦力为零,对小物体,从P到C应用机械能守恒定律有:
mgh=
mv12,解得h=
R
则PQ的距离为H=h+ymin=R.
答:PQ的距离为R.
水平方向:R=vt,竖直下落的高度为y=
| 1 |
| 2 |
则y=
| gR2 |
| 2v2 |
由此可知经过C点的速度越大,下落高度越小,QA距离越大,所以通过C点的速度最小时,QA的距离最小,设小物体经过C点时的速度最小为v1.
根据牛顿第二定律有:
mg=
| mv12 |
| R |
此时ymin=
| gR2 |
| 2v12 |
| 1 |
| 2 |
设PC高度差为h,因为小物体对竖直墙的压力为零,所以小物体受到墙的摩擦力为零,对小物体,从P到C应用机械能守恒定律有:
mgh=
| 1 |
| 2 |
| 1 |
| 2 |
则PQ的距离为H=h+ymin=R.
答:PQ的距离为R.

练习册系列答案
相关题目
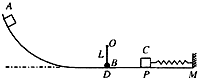 如图所示,竖直放置的圆弧轨道和水平轨道两部分相连. 水平轨道的右侧有一质量为 2m 的滑块C 与轻质弹簧的一端相连,弹簧的另一端固定在竖直的墙M上,弹簧处于原长时,滑块C静止在P 点处;在水平轨道上方O 处,用长为L 的细线悬挂一质量为 m 的小球B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动.质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生弹性碰撞. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为μ=0.5,A、B、C 均可视为质点,重力加速度为g.
如图所示,竖直放置的圆弧轨道和水平轨道两部分相连. 水平轨道的右侧有一质量为 2m 的滑块C 与轻质弹簧的一端相连,弹簧的另一端固定在竖直的墙M上,弹簧处于原长时,滑块C静止在P 点处;在水平轨道上方O 处,用长为L 的细线悬挂一质量为 m 的小球B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动.质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生弹性碰撞. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为μ=0.5,A、B、C 均可视为质点,重力加速度为g. 如图所示,竖直墙上A点用AB细线悬挂一个光滑小球,小球质量为m=3kg,半径r=0.3m,细线AB长L=0.2m,C为接触点,求:
如图所示,竖直墙上A点用AB细线悬挂一个光滑小球,小球质量为m=3kg,半径r=0.3m,细线AB长L=0.2m,C为接触点,求: 如图所示,竖直墙和3/4光滑圆轨道相切于A点,圆轨道的最低点为B、最高点为C、圆心为O、半径为R,小物体从紧贴墙的位置P由静止释放,欲使小物体不离开圆轨道,最终打在竖直墙上位置Q(图中未画出)处,并且QA距离最小,求PQ的距离.
如图所示,竖直墙和3/4光滑圆轨道相切于A点,圆轨道的最低点为B、最高点为C、圆心为O、半径为R,小物体从紧贴墙的位置P由静止释放,欲使小物体不离开圆轨道,最终打在竖直墙上位置Q(图中未画出)处,并且QA距离最小,求PQ的距离.