题目内容
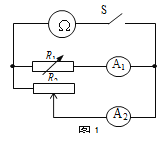
【题目】如图所示,质量为M=3kg的平板小车置于光滑水平面上,其右端与一个固定的半径为R=0.8m的四分之一光滑圆弧轨道等高对接。小车上表面两侧区域光滑,中间为长度l=0.8m的粗糙区域,摩擦因数![]() =0.25,小车上表面左端固定一轻弹簧,弹簧原长小于左侧光滑区域的长度。现将一质量为m=1Kg的小物块(可视为质点)从圆弧轨道最高点由静止释放(g取10m/s2,忽略物块与轻弹簧碰撞时的能量损失)。求:
=0.25,小车上表面左端固定一轻弹簧,弹簧原长小于左侧光滑区域的长度。现将一质量为m=1Kg的小物块(可视为质点)从圆弧轨道最高点由静止释放(g取10m/s2,忽略物块与轻弹簧碰撞时的能量损失)。求:
(1)物块在圆弧轨道最低点时受到的支持力;
(2)轻弹簧的最大弹性势能;
(3)要保证小物块不从小车上滑落,粗糙区域长度x应满足的条件。

【答案】(1)30N(2)4J(3)![]()
【解析】 (1)物块从圆弧轨道的最高点滑到最低点的过程中,只有重力做功,机械能守恒,则由机械能守恒定律得:
![]()
代入数据解得:v=4m/s,
在最低点,合力提供向心力: ![]()
代入数据解得:T=30N。
(2)物块滑上平板车后,由于水平面光滑,系统的合外力为零,所以物块和平板车组成的系统动量守恒。速度相等时,弹簧的压缩量最大,以向右为正方向,由动量守恒定律得:
mv=(m+M)v共,
代入数据解得:v共=1m/s;
根据能量守恒定律得: ![]()
代入数据解得:EPm=4J;
(3)要保证小物块不从小车上滑落,小物块被弹簧弹回后,到达粗糙区域右侧时速度刚好与小车相等,设粗糙区域长度为x
根据能量守恒定律得: ![]()
代入数据解得: ![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目