Question

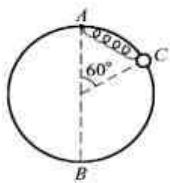如图所示，光滑圆环固定在竖直平面内，一劲度系数k=120N/m的轻质弹簧，一端系于圆环的最高点A，另一端系一套在圆环上质量m=5kg的小球，已知环半径R=0.5m，弹簧原长L₀=0.5m．小球从图中位置C由静止释放滑至最低点B时，测得其速度v_B=3m/s．求：
（1）在此过程中弹簧弹力做的功；
（2）球经过B点时对环的作用力．

Answer 1

分析：（1）球由C到B的过程，重力和弹簧的弹力做功，设弹簧弹力做功为W，写出动能定律的方程，代入数据即可；
（2）小球在最低点时，重力、弹簧的弹力和环对球的作用力提供向心力，写出方程，代入数据即可．

解答：解：（1）球由C到B的过程，设弹簧弹力做功为W，则mgR(1+cos60°)+w=

1

2

mv2
解得：W=-15J
（2）球经B点时弹簧的伸长量x=2R-L₀=0.5m
设环对球的作用力向上，大小为F，那么kx+F-mg=m

v2

R

解得：F=80N 方向向上
由牛顿第三定律，球对环的作用力为F'=80N方向向下
答：（1）在此过程中弹簧弹力做的功为-15J；
（2）球经过B点时对环的作用力为80N．

点评：该题中正确计算出重力和弹力做的功 是解题的关键．该题属于基础题目．