题目内容
【题目】如图所示,一质量m=2kg的木箱静止在粗糙水平面上。从t=0开始,木箱受到F=10N、与水平面的夹角为θ=37°的恒定拉力,沿水平面匀加速运动。已知木箱与水平面间的动摩擦因数μ=0.2,重力加速度g=10m/s2,sin37°= 0.6,cos37°= 0.8。

(1)画出木箱受力的示意图;
(2)求木箱的加速度a的大小;
(3)求0~2s时间内,木箱位移x的大小。
【答案】(1) (2)2.6m/s2(3)5.2m
(2)2.6m/s2(3)5.2m
【解析】
(1)木箱受力如下图所示:
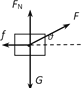
(2)对木箱受力分析,在竖直方向: FN+Fsinθ-mg=0
在水平方向:Fcosθ-f=ma
又因为摩擦力f=μFN
解得加速度a = 2.6m/s2
(3)根据匀变速直线运动位移和时间的关系,![]()
解得x =5.2m。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在研究平抛运动的实验中,某同学记录了小球运动过程中经过的A、B、C、D、E、F、G点的位置,相邻两点的时间间隔均为![]() =0.05s。取A点为坐标原点,以+x方向表示水平初速度方向,以+y方向表示竖直向下方向,实验记录如下表。
=0.05s。取A点为坐标原点,以+x方向表示水平初速度方向,以+y方向表示竖直向下方向,实验记录如下表。
标号n | A | B | C | D | E | F | G |
t/s | 0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
x/m | 0 | 0.024 | 0.051 | 0.073 | 0.098 | 0.126 | 0.150 |
y/m | 0 | 0.042 | 0.108 | 0.198 | 0.314 | 0.454 | 0.617 |

(1)作出x—t图象如图甲所示,小球平抛运动的水平初速度大小是_______m/s;
(2)根据表格中数据可知,t=0.10s时,小球的竖直分速度大小是____________m/s;
(3)以t为横坐标,![]() 为纵坐标,作出
为纵坐标,作出![]() —t图象如图11乙所示,可得直线斜率的数值k=4.86,其单位是__________,该处重力加速度g=____________m/s2。
—t图象如图11乙所示,可得直线斜率的数值k=4.86,其单位是__________,该处重力加速度g=____________m/s2。