题目内容
14.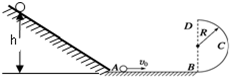 质量的金属小球从距水平面的光滑斜面上由静止开始释放,运动到A点时无能量损耗,水平面的粗糙平面,与半径为的光滑的半圆形轨道BCD相切于B点,其中圆轨道在竖直平面内,D为轨道的最高点,小球恰能通过最高点D,完成以下要求(g=10m/s2)
质量的金属小球从距水平面的光滑斜面上由静止开始释放,运动到A点时无能量损耗,水平面的粗糙平面,与半径为的光滑的半圆形轨道BCD相切于B点,其中圆轨道在竖直平面内,D为轨道的最高点,小球恰能通过最高点D,完成以下要求(g=10m/s2)(1)小球运动到A点时的速度为多大?
(2)小球从A运动到B时摩擦阻力所做的功
(3)小球从D点飞出后落点E与A相距多少米?
分析 (1)由动能定理即可求出到A点的速度大小;
(2)小球恰能通过最高点D,求出小球在B点的速度,对AB段由动能定理即可求出摩擦力所做的功;
(3)小球从D点飞出后做平抛运动,根据平抛知识即可求出水平位移
解答 解(1)根据题意和图形可得;物体下落到A点时由动能定律得:
W=mgh=$\frac{1}{2}{mv}_{A}^{2}$
所以vA=$\sqrt{2gh}=\sqrt{2×10×2}m/s=2\sqrt{10}m/s$
(2)物体运动到D点时:F向=mg=$\frac{{mv}_{D}^{2}}{R}$
解得:vD=$\sqrt{gR}$=2m/s
当物体由B运动到D点时机械能守恒定律得:$\frac{1}{2}{mv}_{B}^{2}=mg×2R+\frac{1}{2}{mv}_{D}^{2}$
v B=$\sqrt{4gR{+v}_{D}^{2}}$=2$\sqrt{5}$m/s
所以A到B时:Wμ=$\frac{1}{2}{mv}_{B}^{2}-\frac{1}{2}{mv}_{A}^{2}$=-1J
(3)物体从D点飞出后做平抛运动,故有:h=2R=$\frac{1}{2}g{t}^{2}$
解得:t=$\sqrt{\frac{4R}{g}}$═0.4s
水平位移xBE=vDt=0.8m
所以xAE=AB-xBE=1.2m
答:(1)小球运动到A点的速度为$2\sqrt{10}$m/s;
(2)小球从A运动到B时摩擦阻力所做的功为-1J;
(3)小球从D点飞出后落点E与A相距1.2m
点评 此题考查复杂运动的分析,考察了动能定理、机械能守恒及平抛运动的知识,难度适中.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
19. 如图所示,虚线框内为一电压表的原理图,灵敏电流计G的内阻为R,AB是一根长为L、粗细均匀、电阻为50R的电阻丝,调节滑动触点P的位置,可改变电压表的量程,先将P出点由距A端0.1L处移至0.8L处,电压表的量程将扩大为原来的( )
如图所示,虚线框内为一电压表的原理图,灵敏电流计G的内阻为R,AB是一根长为L、粗细均匀、电阻为50R的电阻丝,调节滑动触点P的位置,可改变电压表的量程,先将P出点由距A端0.1L处移至0.8L处,电压表的量程将扩大为原来的( )
 如图所示,虚线框内为一电压表的原理图,灵敏电流计G的内阻为R,AB是一根长为L、粗细均匀、电阻为50R的电阻丝,调节滑动触点P的位置,可改变电压表的量程,先将P出点由距A端0.1L处移至0.8L处,电压表的量程将扩大为原来的( )
如图所示,虚线框内为一电压表的原理图,灵敏电流计G的内阻为R,AB是一根长为L、粗细均匀、电阻为50R的电阻丝,调节滑动触点P的位置,可改变电压表的量程,先将P出点由距A端0.1L处移至0.8L处,电压表的量程将扩大为原来的( )| A. | 3.4倍 | B. | 6.8倍 | C. | 8倍 | D. | 4倍 |
2.以下说法正确的是( )
| A. | 新闻联播节目19点开播,19点指时间间隔 | |
| B. | 第3秒是指时刻 | |
| C. | 出租车的收费标准有2.00元/公里,其中的“公里”指的是路程 | |
| D. | 位移是矢量,而路程是标量 |
9.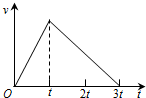 一辆汽车从甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示.那么0~t和t~3t两段时间内,( )
一辆汽车从甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示.那么0~t和t~3t两段时间内,( )
 一辆汽车从甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示.那么0~t和t~3t两段时间内,( )
一辆汽车从甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示.那么0~t和t~3t两段时间内,( )| A. | 加速度的大小之比为1:2 | |
| B. | 位移的大小之比为1:2 | |
| C. | 平均速度的大小之比为2:1 | |
| D. | 各自中间时刻速度的大小之比为1:1 |
19.下列说法正确的是( )
| A. | 电场线并不真实存在,它其实是电荷只在电场力作用下的运动轨迹 | |
| B. | 电场中某点的电场强度在数值上等于单位电荷在该点受到的电场力大小 | |
| C. | 电荷在某点的电势能,等于把它从该点移到零电势位置电场力做的功 | |
| D. | 以无穷远处为零电势,负检验电荷在正点电荷附近的电势能总是负的 |


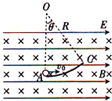 如图所示,某空间内存在着正交的匀强电场和匀强磁场,电场强度的方向水平向右,磁感应强度的方向垂直纸面向里,匀强磁场的磁感应强度的大小B=0.1T.一段光滑绝缘的圆弧轨道AC固定在复合场中,圆弧轨道所在的平面为竖直平面,且与电场度的方向平行,圆弧的圆心为O、半径R=1.8m,连结OA在竖直方向上,圆弧轨道所对应的圆心角θ=37°.现有一质量m=3.6×10-5kg、电荷量q=9.0×10-4C的带正电的小球(可视为质点)以EK0的初动能沿水平方向由A点射入圆弧轨道,一段时间后小球从C点离开圆弧轨道,此刻将电场强度的方向改为竖直方向,大小保持不变,小球离开C点后仍沿该圆弧轨道所在的圆周做匀速圆周运动,不计空气阻力,已知sin37°=0.6,cos37°=0.8,g=10m/s2,求:
如图所示,某空间内存在着正交的匀强电场和匀强磁场,电场强度的方向水平向右,磁感应强度的方向垂直纸面向里,匀强磁场的磁感应强度的大小B=0.1T.一段光滑绝缘的圆弧轨道AC固定在复合场中,圆弧轨道所在的平面为竖直平面,且与电场度的方向平行,圆弧的圆心为O、半径R=1.8m,连结OA在竖直方向上,圆弧轨道所对应的圆心角θ=37°.现有一质量m=3.6×10-5kg、电荷量q=9.0×10-4C的带正电的小球(可视为质点)以EK0的初动能沿水平方向由A点射入圆弧轨道,一段时间后小球从C点离开圆弧轨道,此刻将电场强度的方向改为竖直方向,大小保持不变,小球离开C点后仍沿该圆弧轨道所在的圆周做匀速圆周运动,不计空气阻力,已知sin37°=0.6,cos37°=0.8,g=10m/s2,求: 某电视剧拍摄现场,导演要拍摄摩托车与小轿车的追及场面,道具制作了摩托车与小轿车遥控模型.两车在同一直线轨道上同向匀速行驶,“摩托车”在“小轿车”的后面,两车相距L=1.5m时,两车同时开始刹车,刹车后“摩托车”的速度一时间图象如图所示,“小轿车”的速度与时间的关系为v2=3-0.25t(v2的单位为m/s,t的单位为s),求:
某电视剧拍摄现场,导演要拍摄摩托车与小轿车的追及场面,道具制作了摩托车与小轿车遥控模型.两车在同一直线轨道上同向匀速行驶,“摩托车”在“小轿车”的后面,两车相距L=1.5m时,两车同时开始刹车,刹车后“摩托车”的速度一时间图象如图所示,“小轿车”的速度与时间的关系为v2=3-0.25t(v2的单位为m/s,t的单位为s),求: 如图所示,厚度为d的玻璃砖与水平实验桌面成45°角放置.红色激光束平行于水平桌面射到玻璃砖的表面,在桌面上得到两个光点A、B,已知玻璃砖对该红色激光的折射率为$\sqrt{2}$.求:AB间的距离L.
如图所示,厚度为d的玻璃砖与水平实验桌面成45°角放置.红色激光束平行于水平桌面射到玻璃砖的表面,在桌面上得到两个光点A、B,已知玻璃砖对该红色激光的折射率为$\sqrt{2}$.求:AB间的距离L.