题目内容
2.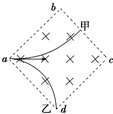 两个电荷量、质量均相同的带电粒子甲、乙以不同速率从a点沿对角线方向射入正方形匀强磁场中,磁场方向垂直纸面向里.甲粒子垂直bc离开磁场,乙粒子垂直ac从d点离开磁场,不计粒子重力,则( )
两个电荷量、质量均相同的带电粒子甲、乙以不同速率从a点沿对角线方向射入正方形匀强磁场中,磁场方向垂直纸面向里.甲粒子垂直bc离开磁场,乙粒子垂直ac从d点离开磁场,不计粒子重力,则( )| A. | 甲粒子带负电,乙粒子带正电 | |
| B. | 甲粒子的运行动能是乙粒子运行动能的2倍 | |
| C. | 甲粒子所受洛伦兹力是乙粒子所受洛伦兹力的2倍 | |
| D. | 甲粒子在磁场中的运行时间与乙粒子相等 |
分析 根据粒子运动轨迹,应用左手定则可以判断出粒子的电性;
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据题意求出粒子轨道半径关系,然后应用牛顿第二定律求出粒子的速度然后分析答题;根据粒子做圆周运动的周期公式与粒子转过的圆心角求出粒子的运动时间.
解答 解:A、由左手定则可判定甲粒子带正电,乙粒子带负电,故A错误;
B、令正方形磁场的边长为L,则由题知甲粒子运行的半径为$\sqrt{2}$L,乙粒子运行的半径为$\frac{\sqrt{2}}{2}$L,由洛伦兹力提供向心力有Bqv=m$\frac{v2}{r}$,动能Ek=$\frac{1}{2}$mv2=$\frac{{B}^{2}{q}^{2}{r}^{2}}{2m}$,甲粒子的运行动能是乙粒子运行动能的4倍,故B错误;
C、由牛顿第二定律得:Bqv=m$\frac{v2}{r}$,解得:F=Bqv=$\frac{{B}^{2}{q}^{2}r}{m}$,所以甲粒子在磁场中所受洛伦兹力是乙粒子所受洛伦兹力的2倍,故C正确;
D、粒子的运动时间:t=$\frac{θ}{360°}$•$\frac{2πm}{Bq}$,甲粒子运行轨迹所对圆心角为45°,乙粒子运行轨迹所对圆心角为90°,即甲粒子在磁场中的运行时间是乙粒子的一半,故D错误;
故选:C.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程是解题的关键,应用牛顿第二定律与粒子做圆周运动的周期公式可以解题.

练习册系列答案
相关题目
10.下列关于加速度和速度的描述中,正确的是( )
| A. | 速度变化越大,加速度就越大 | |
| B. | 当加速度与速度方向相同且又减小时,物体做减速运动 | |
| C. | 加速度的方向与速度变化的方向可以相同也可以相反 | |
| D. | 速度变化越快,加速度越大 |
7.下列说法正确的是( )
| A. | 空气的绝对湿度大,相对湿度一定大 | |
| B. | 上午十时,教室内空气中的氮气和氧气的分子平均动能相同 | |
| C. | 荷叶上的小水滴呈球形,这是表面张力使液面收缩的结果 | |
| D. | 有一分子a从无穷远处靠近固定不动的分子b,当a、b间分子力为零时,它们具有的分子势能一定最小 | |
| E. | 一定质量的理想气体等温膨胀,可能会向外散热 |
11.如图所示,把一个带负电的小球放入原来不带电的金属空腔球壳内并与内壁接触,其结果是( ) 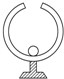

| A. | 只有球壳外表面带负电 | |
| B. | 只有球壳内表面带负电 | |
| C. | 球壳的内表面带正电,外表面带负电 | |
| D. | 小球带负电,球壳内外表面都不带电 |
12. 如图所示,边长为L的正方形ABCD区域内存在磁感应强度方向垂直于纸面向里,大小为B的匀强磁场,一质量为m,带电荷量为-q的粒子从AB边的中点处垂直于磁感应强度方向射入磁场,速度方向与AB边的夹角为30°,若要求该粒子不从AD边射出磁场,则其速度大小应满足( )
如图所示,边长为L的正方形ABCD区域内存在磁感应强度方向垂直于纸面向里,大小为B的匀强磁场,一质量为m,带电荷量为-q的粒子从AB边的中点处垂直于磁感应强度方向射入磁场,速度方向与AB边的夹角为30°,若要求该粒子不从AD边射出磁场,则其速度大小应满足( )
 如图所示,边长为L的正方形ABCD区域内存在磁感应强度方向垂直于纸面向里,大小为B的匀强磁场,一质量为m,带电荷量为-q的粒子从AB边的中点处垂直于磁感应强度方向射入磁场,速度方向与AB边的夹角为30°,若要求该粒子不从AD边射出磁场,则其速度大小应满足( )
如图所示,边长为L的正方形ABCD区域内存在磁感应强度方向垂直于纸面向里,大小为B的匀强磁场,一质量为m,带电荷量为-q的粒子从AB边的中点处垂直于磁感应强度方向射入磁场,速度方向与AB边的夹角为30°,若要求该粒子不从AD边射出磁场,则其速度大小应满足( )| A. | v≤$\frac{2qBL}{m}$ | B. | v≥$\frac{2qBL}{m}$ | C. | v≤$\frac{qBL}{m}$ | D. | v≥$\frac{qBL}{m}$ |
 如图所示,在正的点电荷Q的电场中有a、b两点,它们到点电荷Q的距离r1<r2,a、b两点间的电势差为100V.求
如图所示,在正的点电荷Q的电场中有a、b两点,它们到点电荷Q的距离r1<r2,a、b两点间的电势差为100V.求 实验课上老师布置两项任务,①测量一个电流计的内电阻,②测量干电池的电动势和内阻,实验台上准备了如下器材:
实验课上老师布置两项任务,①测量一个电流计的内电阻,②测量干电池的电动势和内阻,实验台上准备了如下器材: