题目内容
16.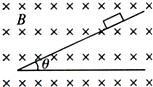 质量为m,带电量为q的小物块,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,磁感应强度为B,如图所示,求:
质量为m,带电量为q的小物块,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,磁感应强度为B,如图所示,求:(1)带电小物块下滑后某时刻对斜面的作用力恰好为零时小物块的速度;
(2)小物块在斜面上运动的距离.
分析 带电小物块下滑后某时刻对斜面的压力恰好为零时,洛伦兹力与重力垂直于斜面向下的分力大小相等,列出方程.由于洛伦兹力不做功,小物块的机械能守恒,据此列式,联立即可求解.
解答 解:当小物块离开斜面时,对其进行受力分析,将重力分解,由题意知:
Bqv=mgcosθ…①
小物块沿斜面向下运动过程中机械能守恒:
mgSsinθ=$\frac{1}{2}$mv2…②
联立①②式得:
v=$\frac{mgcosθ}{qB}$
S=$\frac{{m}^{2}gco{s}^{2}θ}{2{B}^{2}{q}^{2}sinθ}$
答:(1)带电小物块下滑后某时刻对斜面的作用力恰好为零时小物块的速度$\frac{mgcosθ}{qB}$;
(2)小物块从开始至此过程中沿斜面下滑的距离为$\frac{{m}^{2}gco{s}^{2}θ}{2{B}^{2}{q}^{2}sinθ}$.
点评 解决本题的关键是正确地进行受力分析,抓住垂直于斜面方向上的合力为零,运用机械能守恒定律进行求解.

练习册系列答案
相关题目
6. 如图所示,光滑导轨倾斜放置,其下端连接一个灯泡,匀强磁场垂直于导轨所在平面,当ab棒下滑到稳定状态时,小灯泡获得的功率为P0.除灯泡外,其它电阻不计,要使灯泡的功率变为2P0(仍在灯泡额定功率范围内),下列措施正确的是( )
如图所示,光滑导轨倾斜放置,其下端连接一个灯泡,匀强磁场垂直于导轨所在平面,当ab棒下滑到稳定状态时,小灯泡获得的功率为P0.除灯泡外,其它电阻不计,要使灯泡的功率变为2P0(仍在灯泡额定功率范围内),下列措施正确的是( )
 如图所示,光滑导轨倾斜放置,其下端连接一个灯泡,匀强磁场垂直于导轨所在平面,当ab棒下滑到稳定状态时,小灯泡获得的功率为P0.除灯泡外,其它电阻不计,要使灯泡的功率变为2P0(仍在灯泡额定功率范围内),下列措施正确的是( )
如图所示,光滑导轨倾斜放置,其下端连接一个灯泡,匀强磁场垂直于导轨所在平面,当ab棒下滑到稳定状态时,小灯泡获得的功率为P0.除灯泡外,其它电阻不计,要使灯泡的功率变为2P0(仍在灯泡额定功率范围内),下列措施正确的是( )| A. | 换一个电阻为原来一半的灯泡 | B. | 磁感应强度增为原来的2倍 | ||
| C. | 换一根质量为原来的$\sqrt{2}$倍的金属棒 | D. | 把导轨间的距离增大为原来的$\sqrt{2}$倍 |
7. 如图所示,从同一栋楼的不同高度水平抛出相同质量的物体,所有物体落在地面上的同一点P,取地面为重力势能为零的平面,则下列说法正确的是( )
如图所示,从同一栋楼的不同高度水平抛出相同质量的物体,所有物体落在地面上的同一点P,取地面为重力势能为零的平面,则下列说法正确的是( )
 如图所示,从同一栋楼的不同高度水平抛出相同质量的物体,所有物体落在地面上的同一点P,取地面为重力势能为零的平面,则下列说法正确的是( )
如图所示,从同一栋楼的不同高度水平抛出相同质量的物体,所有物体落在地面上的同一点P,取地面为重力势能为零的平面,则下列说法正确的是( )| A. | 从高度越大的楼层抛出的物体,落地过程中重力做功越多 | |
| B. | 从高度较大的楼层抛出的物体,落地时动能较大 | |
| C. | 从高度较大的楼层抛出的物体,落地时机械能较大 | |
| D. | 从不同楼层抛出的物体,落地时动能可能不同 |
4. 带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )
带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )
 带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )
带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )| A. | 若Bqv<K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向里 | B. | 若Bqv<K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向外 | ||
| C. | 若Bqv>K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向里 | D. | 若Bqv>K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向外 |
20. 钢制单摆小环用绝缘细线悬挂,置于如图所示的匀强磁场中将小球拉离平衡位置由静止释放,经足够长的运动时间后,以下说法正确的是(忽略空气阻力)( )
钢制单摆小环用绝缘细线悬挂,置于如图所示的匀强磁场中将小球拉离平衡位置由静止释放,经足够长的运动时间后,以下说法正确的是(忽略空气阻力)( )
 钢制单摆小环用绝缘细线悬挂,置于如图所示的匀强磁场中将小球拉离平衡位置由静止释放,经足够长的运动时间后,以下说法正确的是(忽略空气阻力)( )
钢制单摆小环用绝缘细线悬挂,置于如图所示的匀强磁场中将小球拉离平衡位置由静止释放,经足够长的运动时间后,以下说法正确的是(忽略空气阻力)( )| A. | 多次往返后,最后静止在最低点平衡位置 | |
| B. | 多次往返后,部分机械能转化为内能 | |
| C. | 最后小球在磁场中一直振动 | |
| D. | 最后小球在磁场中运动的过程中,通过最低点时合外力方向有时向上,有时向下,有时为零 |
 在如图所示的电路中,电源内电阻r=3Ω,当开关S闭合后电路正常工作,电压表的读数U=6V,电流表的读数I=1A.则电阻R=6Ω,电源电动势E=9V.
在如图所示的电路中,电源内电阻r=3Ω,当开关S闭合后电路正常工作,电压表的读数U=6V,电流表的读数I=1A.则电阻R=6Ω,电源电动势E=9V.