题目内容
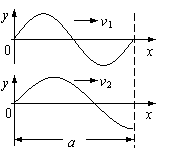
两列平面简谐波以不同速度沿x方向传播，右图是 t=0 时刻这两列波在长a的区域内的波形．设 t=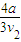
时刻该区域又一次出现相同的波形，则这两列波的速度 v1与v2的大小之比可能是（ ）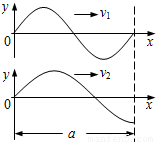
A．1：3
B．3：1
C．2：3
D．3：2
【答案】分析：由图可读出波长，根据波速公式v=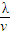
得到两列波周期的表达式．由题分析两列波的周期与时间t的关系，得到波速关系的通项，即可求解．
解答：解：由图象得知，两列波的波长分别为：
λ1=a，λ2=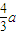
两列波的周期分别为：
=
，
=
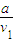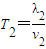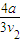
故t=T2=nT1，
由上得到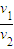
=
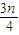（n=1，2，3…）
当n=4时，到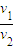
=
；当n=2时，
=
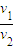，由于n是整数，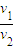
不可能是
和
．
故选BD
点评：本题的解题关键是抓住波的周期性，得到两列波波速关系的通项，再求解特殊值．
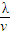得到两列波周期的表达式．由题分析两列波的周期与时间t的关系，得到波速关系的通项，即可求解．解答：解：由图象得知，两列波的波长分别为：
λ1=a，λ2=
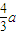
两列波的周期分别为：
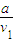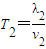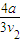
=，=故t=T2=nT1，
由上得到
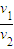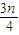=（n=1，2，3…）当n=4时，到
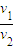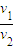=；当n=2时，=，由于n是整数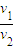，不可能是和．故选BD
点评：本题的解题关键是抓住波的周期性，得到两列波波速关系的通项，再求解特殊值．
练习册系列答案
相关题目
（2006?黄浦区模拟）两列平面简谐波以不同速度沿x方向传播，右图是 t=0 时刻这两列波在长a的区域内的波形．设 t=
C．如图为一列沿x轴正方向传播的简谐波在t=0时刻的波形图，已知波速为10m/s，则图中x=4m处的P质点振动方程为
； 
D.用同一装置进行双缝干涉实验，蓝光的相邻条纹间距较大。
。在此截面所在的平面内，一条光线以45o的入射角从AC边的中点M射入棱镜，求射出点的位置（不考虑光线沿原来路返回的情况）。
C．通过电子双缝实验，发现电子的干涉现象
→
．若
和
迎面碰撞，初速度大小分别为v1、v2，
He、
的质量分别为m1、m2、m3、m4，反应后
时刻这两列波在长a的区域内的波形. 设
时刻该区域又一次出现相同的波形，则这两列波的速度v1与v2的大小之比可能是