题目内容
(11分)如图所示,绝缘光滑水平轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接,圆弧的半径R=0.40m。在轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104N/C。现有一质量m=0.10kg的带电体(可视为质点)放在水平轨道上与B端距离s=1.0m的位置,由于受到电场力的作用带电体由静止开始运动,当运动到圆弧形轨道的C端时,速度恰好为零。已知带电体所带电荷量q=8.0×10-5C,求:
(1)带电体运动到圆弧形轨道的B端时对圆弧轨道的压力;
(2)带电体沿圆弧形轨道从B端运动到C端的过程中,摩擦力做的功。

|
(11分)
(1)设带电体在水平轨道上运动的加速度大小为a,
根据牛顿第二定律有qE = ma
解得![]() m/s2..........1分
m/s2..........1分
设带电体运动到B端的速度大小为vB,则![]()
解得![]() m/s ..........1分
m/s ..........1分
(另解:由![]() 得 ..........1分
得 ..........1分
解得![]() m/s ..........1分)
m/s ..........1分)
设带电体运动到圆轨道B端时受轨道的支持力为N,根据牛顿第二定律有
![]() ..........1分
..........1分
解得![]() N ..........1分
N ..........1分
根据牛顿第三定律可知,带电体对圆弧轨道B端的压力大小![]() N
N
方向:竖直向下..........1分
(2)因电场力做功与路径无关,所以带电体沿圆弧形轨道运动过程中,
电场力所做的功![]() J ..........1分
J ..........1分
设带电体沿圆弧形轨道运动过程中摩擦力所做的功为W摩,对此过程根据动能定理有
![]() ..........2分
..........2分
解得 W摩 =-0.72J ..........1分

 阅读快车系列答案
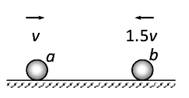
阅读快车系列答案 如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( )
如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( ) (2011?翠屏区模拟)如图所示,在光滑绝缘的水平台面上,存在平行于水平面向右的匀强电场,电场强度为E.水平台面上放置两个静止的小球A和B(均可看作质点),两小球质量均为m,A球带电荷量为+Q,B球不带电,A、B连线与电场线平行.开始时两球相距L,在电场力作用下,A球开始运动(此时为计时零点,即t=0),后与B球发生对心碰撞,碰撞过程中A、B两球总动能无损失,设在各次碰撞过程中,A、B两球间无电量转移,且不考虑两球碰撞时间及两球间的万有引力,试求:
(2011?翠屏区模拟)如图所示,在光滑绝缘的水平台面上,存在平行于水平面向右的匀强电场,电场强度为E.水平台面上放置两个静止的小球A和B(均可看作质点),两小球质量均为m,A球带电荷量为+Q,B球不带电,A、B连线与电场线平行.开始时两球相距L,在电场力作用下,A球开始运动(此时为计时零点,即t=0),后与B球发生对心碰撞,碰撞过程中A、B两球总动能无损失,设在各次碰撞过程中,A、B两球间无电量转移,且不考虑两球碰撞时间及两球间的万有引力,试求: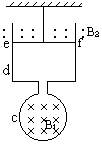 如图所示,由光滑硬导线制成并连接在一起的圆线圈c和线框d被固定在竖直平面内,线圈c所围面积为S,其中的磁场从图中看垂直于纸面向里,磁感应强度为
如图所示,由光滑硬导线制成并连接在一起的圆线圈c和线框d被固定在竖直平面内,线圈c所围面积为S,其中的磁场从图中看垂直于纸面向里,磁感应强度为