��Ŀ����
 ��2011?������ģ�⣩��ͼ��ʾ���ڹ⻬��Ե��ˮƽ̨���ϣ�����ƽ����ˮƽ�����ҵ���ǿ�糡���糡ǿ��ΪE��ˮƽ̨���Ϸ���������ֹ��С��A��B�����ɿ����ʵ㣩����С��������Ϊm��A��������Ϊ+Q��B���磬A��B������糡��ƽ�У���ʼʱ�������L���ڵ糡�������£�A��ʼ�˶�����ʱΪ��ʱ��㣬��t=0��������B����������ײ����ײ������A��B�����ܶ�������ʧ�����ڸ�����ײ�����У�A��B���������ת�ƣ��Ҳ�����������ײʱ�估��������������������
��2011?������ģ�⣩��ͼ��ʾ���ڹ⻬��Ե��ˮƽ̨���ϣ�����ƽ����ˮƽ�����ҵ���ǿ�糡���糡ǿ��ΪE��ˮƽ̨���Ϸ���������ֹ��С��A��B�����ɿ����ʵ㣩����С��������Ϊm��A��������Ϊ+Q��B���磬A��B������糡��ƽ�У���ʼʱ�������L���ڵ糡�������£�A��ʼ�˶�����ʱΪ��ʱ��㣬��t=0��������B����������ײ����ײ������A��B�����ܶ�������ʧ�����ڸ�����ײ�����У�A��B���������ת�ƣ��Ҳ�����������ײʱ�估����������������������1����һ����ײ����˲��A��B������ٶȸ�Ϊ���
��2���Ӽ�ʱ��㵽����������������ײʱ����������ʱ��Ϊ���٣�
��3����Ҫ��A���˶������ж�����ʼ����ѹ���Ҹպò��뿪ˮƽ���棨v=0ʱ�̳��⣩��������ˮƽ���ڼ�һ��糡�����Ĵų�����д���ų�B��t����ʱ��t�ĺ�����ϵ��
��������1������ţ�ٵڶ��������A��ļ��ٶȣ����ٶ�λ�ƹ�ʽ���A����B����ײǰ���ٶȣ�������ײ������A��B�����ܶ�������ʧ�������ٶȣ�
��2�������ٶȹ�ʽ�����һ����ײʱ�䣮��һ������A����B��λ�����ʱ�������ڶ���ײ����λ���������ڶ�����ײʱ�䣮ͬ������������ײʱ�䣮
��3��Ҫ��A���˶������ж�����ʼ����ѹ���Ҹպò��뿪ˮƽ���棬��������������ƽ�⣮���ù��ɷ��ֱ�����Ӽ�ʱ��㵽����������1����ײ��ι��̡���1����ײ������������2����ײ��ι��̡��ӵ�2����ײ������������3����ײ��ι��̡���A����ֱ������ƽ��õ�B��t����ʱ��t�Ĺ�ϵʽ���ܽ�����ɣ�����ų�B��t����ʱ��t�ĺ�����ϵ��
��2�������ٶȹ�ʽ�����һ����ײʱ�䣮��һ������A����B��λ�����ʱ�������ڶ���ײ����λ���������ڶ�����ײʱ�䣮ͬ������������ײʱ�䣮
��3��Ҫ��A���˶������ж�����ʼ����ѹ���Ҹպò��뿪ˮƽ���棬��������������ƽ�⣮���ù��ɷ��ֱ�����Ӽ�ʱ��㵽����������1����ײ��ι��̡���1����ײ������������2����ײ��ι��̡��ӵ�2����ײ������������3����ײ��ι��̡���A����ֱ������ƽ��õ�B��t����ʱ��t�Ĺ�ϵʽ���ܽ�����ɣ�����ų�B��t����ʱ��t�ĺ�����ϵ��
����⣺��1��A��ļ��ٶ�Ϊa=
��ǰA���ٶ�ΪvA1=
=
����ǰB���ٶ�ΪvB1=0������ײ������A��B�����ܶ�������ʧ�������ٶȣ�����ײ��A��B���ٶȷֱ�
vA1��=0��vB1��=vA1=
��
��2��A��B������һ�Ρ��ڶ��Ρ������ε���ײʱ��ֱ�Ϊt1��t2��t3��
��t1=
=
��һ������t2-t1ʱ��A��B�������ڶ�����ײ������ǰ˲��A��B�����ٶ�ΪvA2��vB2������
vB1�䣨t2-t1��=
a��t2-t1��2
��ã�t2=3t1
vA2=a��t2-t1��=2at1=2vA1=2
��
vB2=vB1��=
��
�ڶ�������˲�䣬A��B�����ٶȷֱ�Ϊ
vA2���vB2�䣬��t3-t2ʱ��A��B��������ײ��������ײǰ˲��A��B�����ٶȷֱ�vA3��vB3
��vA2��=vB2=
��
vB2��=vA2=2
��
��vB2�䣨t3-t2��=vA2�䣨t3-t2��+
a��t3-t2��2������������ײ
��ã�t3-t2=t2-t1��t3=5
��
��3����A��Ҫ��A���˶������ж�����ʼ����ѹ���Ҹպò��뿪ˮƽ���棬��������������ǡ��ƽ�⣬��
BQvA=mg����B=
��A��ļ��ٶ�Ϊ a=
���A��ʼ�˶���������1����ײ��ι����У�
B��t��=
=
0��t��
�ӵ�1����ײ��������2����ײ��ι����У�
B��t��=
��t��3
�ӵ�2����ײ��������3����ײ��ι����У�
B��t��=
3
��t��5
�ӵ�3����ײ��������4����ײ��ι����У�
B��t��=
5
��t��7
��
�Դ����ƣ��ӵ�n����ײ��������n+1����ײ��ι����У�
B��t��=
��2n-1��
��t�ܣ�2n+1��
��n=1��2��3������
��
��1����һ����ײ����˲��A��B������ٶȸ�Ϊ0��
��
��2���Ӽ�ʱ��㵽����������������ײʱ����������ʱ��Ϊ5
��
��3���ų�B��t����ʱ��t�ĺ�����ϵ�� B��t��=
��2n-1��
��t�ܣ�2n+1��
��n=1��2��3��������
| QE |
| m |
��ǰA���ٶ�ΪvA1=
| 2aL |
|
vA1��=0��vB1��=vA1=
|
��2��A��B������һ�Ρ��ڶ��Ρ������ε���ײʱ��ֱ�Ϊt1��t2��t3��
��t1=
| vA1-0 |
| a |
|
��һ������t2-t1ʱ��A��B�������ڶ�����ײ������ǰ˲��A��B�����ٶ�ΪvA2��vB2������
vB1�䣨t2-t1��=
| 1 |
| 2 |
��ã�t2=3t1
vA2=a��t2-t1��=2at1=2vA1=2
|
vB2=vB1��=
|
�ڶ�������˲�䣬A��B�����ٶȷֱ�Ϊ
vA2���vB2�䣬��t3-t2ʱ��A��B��������ײ��������ײǰ˲��A��B�����ٶȷֱ�vA3��vB3
��vA2��=vB2=
|
vB2��=vA2=2
|
��vB2�䣨t3-t2��=vA2�䣨t3-t2��+
| 1 |
| 2 |
��ã�t3-t2=t2-t1��t3=5
|
��3����A��Ҫ��A���˶������ж�����ʼ����ѹ���Ҹպò��뿪ˮƽ���棬��������������ǡ��ƽ�⣬��
BQvA=mg����B=
| mg |
| QvA |
| QE |
| m |
���A��ʼ�˶���������1����ײ��ι����У�
B��t��=
| mg |
| Qat |
| m2g |
| Q2Et |
|
�ӵ�1����ײ��������2����ײ��ι����У�
B��t��=
| m2g | ||||
Q2E(t-
|
|
|
�ӵ�2����ײ��������3����ײ��ι����У�
B��t��=
| m2g | ||||
Q2E(t-2
|
|
|
�ӵ�3����ײ��������4����ײ��ι����У�
B��t��=
| m2g | ||||
Q2E(t-3
|
|
|
��
�Դ����ƣ��ӵ�n����ײ��������n+1����ײ��ι����У�
B��t��=
| m2g | ||||
Q2E(t-n
|
|
|
��
��1����һ����ײ����˲��A��B������ٶȸ�Ϊ0��
|
��2���Ӽ�ʱ��㵽����������������ײʱ����������ʱ��Ϊ5
|
��3���ų�B��t����ʱ��t�ĺ�����ϵ�� B��t��=
| m2g | ||||
Q2E(t-n
|
|
|
������������С���������˶����⣬�ؼ�Ҫ���ù��ɷ��ܽ���ɣ�������ѧ������⣮

��ϰ��ϵ�д�
�����Ŀ
 ��2011?������ģ�⣩��ͼ��ʾ����ֽ������һ��ǿ�糡��һ�������С���������ƣ���һ����F����������ͼ��������A��B�������˶�����֪��F��AB��н�Ϊ�ȣ�AB�����Ϊd��С�������Ϊq�������н�����ȷ���ǣ�������
��2011?������ģ�⣩��ͼ��ʾ����ֽ������һ��ǿ�糡��һ�������С���������ƣ���һ����F����������ͼ��������A��B�������˶�����֪��F��AB��н�Ϊ�ȣ�AB�����Ϊd��С�������Ϊq�������н�����ȷ���ǣ������� ��2011?������ģ�⣩��ͼ��ʾΪ���������ֱ�ΪԲ�������Σ��Ÿ�Ӧǿ����ͬ����ǿ�ų���Բ��ֱ���������εı߳���ȣ��������ӷֱ�����ͬ���ٶ�ͬʱ���������ų������ٶȷ������ų�����ֱ������Բ�δų��ĵ��ӳ��ٶȷ����Բ�ģ����������δų��ĵ��ӳ��ٶȷ���ֱ�ڱ߽磬���е���룮�������ж���ȷ���ǣ�������
��2011?������ģ�⣩��ͼ��ʾΪ���������ֱ�ΪԲ�������Σ��Ÿ�Ӧǿ����ͬ����ǿ�ų���Բ��ֱ���������εı߳���ȣ��������ӷֱ�����ͬ���ٶ�ͬʱ���������ų������ٶȷ������ų�����ֱ������Բ�δų��ĵ��ӳ��ٶȷ����Բ�ģ����������δų��ĵ��ӳ��ٶȷ���ֱ�ڱ߽磬���е���룮�������ж���ȷ���ǣ�������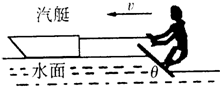 ��2011?������ģ�⣩�����˶���������ͧǣ���˶�Ա��ˮ�ϻ��е�һ���˶����о��������ڽ��л����˶�ʱ��ˮ�Ի����������Fx��ֱ�ڰ��森ij���˶��У�����ͧ��ˮƽǣ���������£��������ˮ��ļнǦ�=37��ʱ����ͼ��ʾ������������v=15m/s���ٶ�������ֱ���˶����˺ͻ����������Ϊ108kg�������������ٶ�gȡ10m/s2��sin37��ȡ
��2011?������ģ�⣩�����˶���������ͧǣ���˶�Ա��ˮ�ϻ��е�һ���˶����о��������ڽ��л����˶�ʱ��ˮ�Ի����������Fx��ֱ�ڰ��森ij���˶��У�����ͧ��ˮƽǣ���������£��������ˮ��ļнǦ�=37��ʱ����ͼ��ʾ������������v=15m/s���ٶ�������ֱ���˶����˺ͻ����������Ϊ108kg�������������ٶ�gȡ10m/s2��sin37��ȡ