��Ŀ����
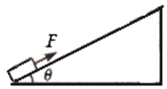
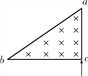
����Ŀ����ͼ��ʾ������M=2kg����L=4��8m��ľ����ˮƽ����F0=66N����������ˮƽ���������ȼ���ֱ���˶�ʱ����������m=1kg�����ǡ���ܾ�ֹ��ľ�����ϣ������������ľ���ڷ��ڵװ��ϣ�ľ����ˮƽ����F=9N���������ɾ�ֹ�������ȼ���ֱ���˶����˶�ʱ��t����ȥ�����������ǡ�����˶���ľ��ǰ������֪ľ����ˮƽ���Ķ�Ħ��������1=0��2�������ľ��װ��Ķ�Ħ��������2�������ľ���ڼ�Ķ�Ħ��������0��![]() ������ľ��ڵĺ�ȡ����Ħ�������ڻ���Ħ������������Ϊ�ʵ㣬ȡg=10m/s2����
������ľ��ڵĺ�ȡ����Ħ�������ڻ���Ħ������������Ϊ�ʵ㣬ȡg=10m/s2����

��1�������ľ��װ��Ķ�Ħ��������2��
��2������F������ʱ��t��
��3���ڶ�������£�������������Ħ������������Q��
���𰸡���1��0��1��2��4s��3��72��0J
��������
�����������1��ˮƽ����F0=66N��ľ��ʱ����ţ�ٵڶ����ɵã�
F0-��1��m+M��g=��m+M��a��
��ù�ͬ�ļ��ٶȣ�a=20m/s2��
�����ľ��֮�����������N=ma0=1��18=20N��
ǡ���ܾ�ֹ����ĺ�ڣ�֪ľ������ֱ�������������ͻ���Ħ����ƽ�⣬������0N=mg��
���ԣ�![]() �����ԣ���2��
�����ԣ���2��![]() ��0=
��0=![]() ��0��5=0��1
��0��5=0��1
��2��ľ�������֮���Ħ������f1=��1��m+M��g=0��2����1+2����10=6N��
�����Ħ��֮��Ļ���Ħ������f2=��2mg=![]() ��1��10=1N��
��1��10=1N��
�����⣬����ȥ��������������ľ����ǰ�˶�����������ܵ���Ħ�����ķ�������ٶȣ�![]()
ľ���ܵ������ľ�������Ħ����������ľ�����ǰ��Ħ���������ٶȣ�![]()
����ľ��ļ��ٶȴ������ļ��ٶȣ���֪ľ����ֹͣ�˶�����ľ��ֹͣ�˶������������ľ��֮���Ħ����С��ľ�������֮������Ħ����������ľ������ڵ��澲ֹ����������ľ���ڻ�����ֱ��ֹͣ��
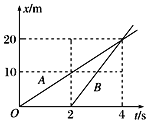
�賷ȥ����ʱľ����ٶ�Ϊv����ȥ������ľ���λ�ƣ�![]() ��
��
�����λ�ƣ�![]()
��x2-x1=L
�����ã�v=4m/s��x1=3��2m��x2=8m
��ȥ����ǰľ������������ܵ�ˮƽ�����͵����Ħ���������ã��ɶ��������ã���F-f1��t=��M+m��v
���ԣ�![]()
��3��ľ�����������ļ��ٶȣ�![]()
�����λ�ƣ�x3��![]() a3t2��
a3t2��![]() ��1��42��8m
��1��42��8m
���ݹ��ܹ�ϵ���������Ĺ����в�����������Q=f1��x1+x3��+f2��x2-x1��
�������ݵã�Q=72��0J

 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�