题目内容
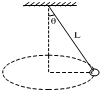
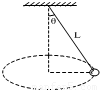
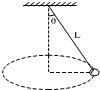在天花板上用一根长为L的细线吊着一个质量为M的小球，使小球做圆锥摆运动，如图，细线与竖直方向的夹角为θ，求小球运动的角速度．分析：小球受重力和拉力，两个力的合力提供向心力，根据牛顿第二定律求出角速度的大小．
解答：解：根据牛顿第二定律得，mgtanθ=mLsinθω2．
ω=
．
答：小球运动的角速度为
．
ω=
|
答：小球运动的角速度为
|
点评：解决本题的关键搞清小球向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
相关题目
用一根长为L的细线，一端固定在天花板上，另一端拴一质量为m的小球，现使细线偏离竖直方向α角后，从A处无初速度释放小球，如图所示，试求：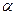
角后，从A处无初速度释放小球，如图所示，试求：
