题目内容
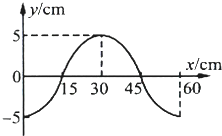 如图所示为一列简谐波的波源O振动1.5s时沿波的传播方向上的波形图,已知波源O在t=0时开始沿y轴负方向振动,t=1.5s时正好第二次到达波谷,则该波的振幅为
如图所示为一列简谐波的波源O振动1.5s时沿波的传播方向上的波形图,已知波源O在t=0时开始沿y轴负方向振动,t=1.5s时正好第二次到达波谷,则该波的振幅为分析:波源做间谐振动,根据振动的周期性和往复性特点得到振动的周期,由波动图象得到波长和振幅的数值,判断振动传到y=5.4m的质点所需的时间,而后求解质点首次到达波峰的时间;波源在一个周期内的路程为振幅的4倍,看此段时间是多少个周期,可求解波源的路程.
解答:解:由波形图得到振幅为5cm;
波源O在t=0时开始沿x轴负方向振动,t=1.5s时它正好第二次到达波谷,由其运动特点得:t=1.25T,
∴T=0.8t=1.2s
由图象可得:λ=60cm=0.6m
而由波传播规律知:
=
∴s=
=0.6×
m=0.75m
即t=1.5s时波刚好传到距波源0.75m的质点,最前面的波峰位于y=0.3m的质点
又∵
=
∴△t=
=(5.4-0.3)×
=10.2s
∴t'=t+△t=1.5+10.2=11.7s
波源的路程:s路=
=
m=1.95m
故答案为:5,11.7,1.95.
波源O在t=0时开始沿x轴负方向振动,t=1.5s时它正好第二次到达波谷,由其运动特点得:t=1.25T,
∴T=0.8t=1.2s
由图象可得:λ=60cm=0.6m
而由波传播规律知:
| S |
| t |
| λ |
| T |
∴s=
| λt |
| T |
| 1.5 |
| 1.2 |
即t=1.5s时波刚好传到距波源0.75m的质点,最前面的波峰位于y=0.3m的质点
又∵
| △S |
| △t |
| λ |
| T |
∴△t=
| △S?T |
| λ |
| 1.2 |
| 0.6 |
∴t'=t+△t=1.5+10.2=11.7s
波源的路程:s路=
| 4At′ |
| T |
| 4×0.05×11.7 |
| 1.2 |
故答案为:5,11.7,1.95.
点评:简谐波的波源做简谐振动,振动周期性的延介质传播,要了解传播的规律,注意波动图象与振动图象的区别

练习册系列答案
相关题目
 如图所示为一列简谐波在t1=0时刻的图象.此时波中质点M的运动方向沿y轴负方向,且t2=0.55s时质点M恰好第3次到达y轴正方向最大位移处.试求:
如图所示为一列简谐波在t1=0时刻的图象.此时波中质点M的运动方向沿y轴负方向,且t2=0.55s时质点M恰好第3次到达y轴正方向最大位移处.试求:
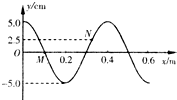 如图所示为一列简谐波在t1=0时刻的图象,此时波中质点M的运动方向沿y轴负方向,且到t2=0.55s质点M恰好第3次到达y轴正方向最大位移处,该波的传播方向为
如图所示为一列简谐波在t1=0时刻的图象,此时波中质点M的运动方向沿y轴负方向,且到t2=0.55s质点M恰好第3次到达y轴正方向最大位移处,该波的传播方向为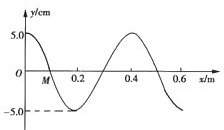 如图所示为一列简谐波在t1=0时刻的图象,已知质点M的振动方程为y=5sin5π(cm).则:
如图所示为一列简谐波在t1=0时刻的图象,已知质点M的振动方程为y=5sin5π(cm).则: