题目内容
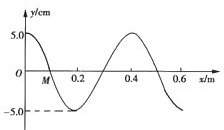 如图所示为一列简谐波在t1=0时刻的图象,已知质点M的振动方程为y=5sin5π(cm).则:
如图所示为一列简谐波在t1=0时刻的图象,已知质点M的振动方程为y=5sin5π(cm).则:(1)此波中质点M在t2等于什么时刻恰好第3次到达y轴正方向最大位移处?
(2)该波的传播方向如何?波速为多大?
分析:(1)通过振动方程求出质点振动的周期以及起振的方向,从而求出质点M在t2等于什么时刻恰好第3次到达y轴正方向最大位移处.
(2)根据质点的振动方向确定波的传播方向,根据波长和周期求出波速的大小.
(2)根据质点的振动方向确定波的传播方向,根据波长和周期求出波速的大小.
解答:解:(1)质点的振动的周期T=
=
=0.4s.质点M的起振方向沿y轴正方向.
可知经过2
周期质点M第3次到达y轴正方向最大位移处.
所以t=2
T=2
×0.4s=0.9s.
(2)因为质点M的振动方向沿y轴正方向,根据上下坡法得,波的传播方向沿x轴正方向.
波长λ=0.4m,则波速v=
=
m/s=1m/s.
答:(1)此波中质点M在t2等于0.9s时刻恰好第3次到达y轴正方向最大位移处.
(2)该波的传播方向沿x轴正方向,波速为1m/s.
| 2π |
| ω |
| 2π |
| 5π |
可知经过2
| 1 |
| 4 |
所以t=2
| 1 |
| 4 |
| 1 |
| 4 |
(2)因为质点M的振动方向沿y轴正方向,根据上下坡法得,波的传播方向沿x轴正方向.
波长λ=0.4m,则波速v=
| λ |
| T |
| 0.4 |
| 0.4 |
答:(1)此波中质点M在t2等于0.9s时刻恰好第3次到达y轴正方向最大位移处.
(2)该波的传播方向沿x轴正方向,波速为1m/s.
点评:解决本题的关键知道波速、波长、周期的关系,以及知道质点振动和波动的关系.

练习册系列答案
相关题目
 如图所示为一列简谐波在t1=0时刻的图象.此时波中质点M的运动方向沿y轴负方向,且t2=0.55s时质点M恰好第3次到达y轴正方向最大位移处.试求:
如图所示为一列简谐波在t1=0时刻的图象.此时波中质点M的运动方向沿y轴负方向,且t2=0.55s时质点M恰好第3次到达y轴正方向最大位移处.试求:
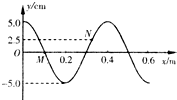 如图所示为一列简谐波在t1=0时刻的图象,此时波中质点M的运动方向沿y轴负方向,且到t2=0.55s质点M恰好第3次到达y轴正方向最大位移处,该波的传播方向为
如图所示为一列简谐波在t1=0时刻的图象,此时波中质点M的运动方向沿y轴负方向,且到t2=0.55s质点M恰好第3次到达y轴正方向最大位移处,该波的传播方向为