题目内容
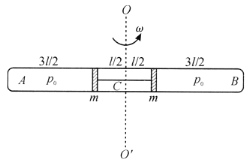
【题目】一水平放置的横截面积为![]() 的两端封闭的玻璃管,其中充满理想气体,现用两个质量同为
的两端封闭的玻璃管,其中充满理想气体,现用两个质量同为![]() ,厚度可略的活塞将该玻璃管分成
,厚度可略的活塞将该玻璃管分成![]() 、
、![]() 、
、![]() 三段,
三段,![]() 段、
段、![]() 段长度同为
段长度同为![]() ,
,![]() 段长度为
段长度为![]() ,两活塞用长为
,两活塞用长为![]() 的不可伸长且不会断裂的轻质细绳相连,三段中的气体压强都为
的不可伸长且不会断裂的轻质细绳相连,三段中的气体压强都为![]() ,如图所示,现将玻璃管以过其中心且垂直于玻璃管的直线
,如图所示,现将玻璃管以过其中心且垂直于玻璃管的直线![]() 为转轴,以角速度
为转轴,以角速度![]() 做匀速转动,假设涉及过程为等温过程,并且各段气体内部的压强差异可略去,气体的质量相对于活塞质量可以忽略
做匀速转动,假设涉及过程为等温过程,并且各段气体内部的压强差异可略去,气体的质量相对于活塞质量可以忽略
(1)角速度![]() 时,求最终两活塞均在管中处于力平衡位置时,除去初态以外
时,求最终两活塞均在管中处于力平衡位置时,除去初态以外![]() 段气体的可能长度(有效数字保留3位)
段气体的可能长度(有效数字保留3位)
(2)角速度![]() 时,求最终两活塞均在管中处于力平衡位置时,除去初态以外
时,求最终两活塞均在管中处于力平衡位置时,除去初态以外![]() 段气体的可能长度(有效数字保留3位)
段气体的可能长度(有效数字保留3位)
【答案】(1) ![]() (2)
(2) ![]() ,
,![]()
【解析】
(1)假设旋转后轻质细绳保持为松弛状态,如图所示,![]() 段气体压强
段气体压强![]() ,长度为
,长度为![]() ,
,![]() 段气体压强
段气体压强![]() ,长度为
,长度为![]() ,
,![]() 段气体压强
段气体压强![]() ,长度为
,长度为![]() .
.
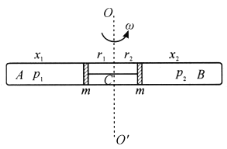
左边活塞与转轴距离为![]() ,右边活塞与转轴距离为
,右边活塞与转轴距离为![]() ,则对
,则对![]() 、
、![]() 、
、![]() 三段气体,由理想气体等温过程性质可得
三段气体,由理想气体等温过程性质可得![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
对转动情况下的活塞运用牛顿第二定律得![]() ,
,![]() .
.
联合以上方程,并令![]() ,
,![]() ,可得
,可得
![]() ,
,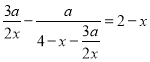 .
.
改写为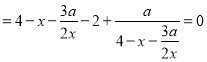 . (*)
. (*)
当![]() 时,
时,![]() ,解上式得两个解
,解上式得两个解![]() ,
,![]() .
.
此时![]() 段气体的长度为
段气体的长度为![]() ,
,
![]() 段气体长度为
段气体长度为![]() ,
,
![]() 段气体长度为
段气体长度为![]() .
.
由以上可知,![]() 时,细绳仍保持松弛,
时,细绳仍保持松弛,![]() 段气体的长度可能为
段气体的长度可能为![]() .
.
此时两活塞都在![]() 的同一侧.
的同一侧.
由于上述方程解中没有出现![]() 段气体长度超过
段气体长度超过![]() 的解,所以绳子不会出现紧绷的情况.
的解,所以绳子不会出现紧绷的情况.
(2)仍假设绳松弛,当![]() 时,
时,![]() ,解(*)式得4个解:
,解(*)式得4个解:
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
对应![]() 段气体长度为
段气体长度为![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 段气体长度为
段气体长度为 ![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 段气体长度为
段气体长度为 ![]() ,
,![]() ,
,![]() ,
,![]() .
.
由以上的分析可知,前两个解对应绳松弛的状态,即![]() 段气体长度为
段气体长度为
![]() ,
,![]() ,
,![]() .
.
此时两个活塞都位于![]() 的同一侧.
的同一侧.
同时注意到有![]() 段长度超过
段长度超过![]() 的解,所以绳子可能会出现紧绷的情况,假设绳子处于紧绷状态,活塞受到的拉力为
的解,所以绳子可能会出现紧绷的情况,假设绳子处于紧绷状态,活塞受到的拉力为![]() ,则活塞的动力学方程变为
,则活塞的动力学方程变为
![]() ,
,![]() .
.
由此同样可得![]() .
.
增加一个几何关系为![]() ,即
,即![]() ,
,
由此可得:![]() .
.
但此时![]() .
.
其中负号表示绳子对活塞的力不是拉力,而是排斥力,这不满足软绳的要求,所以不会出现绳子紧绷的解.
综上,![]() 时,
时,![]() 段气体长度可能为
段气体长度可能为![]() ,
,![]() ,
,![]()