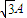题目内容
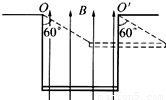
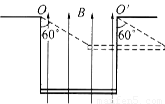
如图,质量为60g的铜棒长为d=20cm,棒的两端用长为L=30cm的细软铜线水平悬挂在磁感应强度为B=0.5T、方向竖直向上的匀强磁场中,当棒中通过恒定电流I后,铜棒向上摆动,最大偏角θ=60°,g取10m/s2,则铜棒中电流I和铜棒在摆动过程中的最大速率v分别为:( )
| A.铜棒中电流I=2A | B.铜棒中电流I=2
| ||
| C.最大速率v≈1m/s | D.最大速率v≈2m/s |

铜棒上摆的过程,根据动能定理得:
FBLsin60°-mgL(1-cos60°)=0,
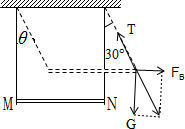
又安培力FB=BId
代入解得,I=2
A
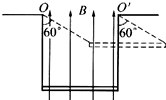
由题意,铜棒向上摆动的最大偏角θ=60°,根据对称性可知,偏角是30°时是其平衡位置,铜棒受力如图所示,则有
G=FBcot30°=
FB ,
当铜棒偏角是30°时,速度最大,动能最大,
由动能定理可得:
m
=FBLsin30°-mgL(1-cos30°)
代入解得,最大速度vm=≈1m/s.
故选BC
FBLsin60°-mgL(1-cos60°)=0,

又安培力FB=BId
代入解得,I=2
| 3 |
由题意,铜棒向上摆动的最大偏角θ=60°,根据对称性可知,偏角是30°时是其平衡位置,铜棒受力如图所示,则有
G=FBcot30°=
| 3 |
当铜棒偏角是30°时,速度最大,动能最大,
由动能定理可得:
| 1 |
| 2 |
| v | 2m |
代入解得,最大速度vm=≈1m/s.
故选BC

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 (2013?静安区二模)如图,质量为60g的铜棒长为d=20cm,棒的两端用长为L=30cm的细软铜线水平悬挂在磁感应强度为B=0.5T、方向竖直向上的匀强磁场中,当棒中通过恒定电流I后,铜棒向上摆动,最大偏角θ=60°,g取10m/s2,则铜棒中电流I和铜棒在摆动过程中的最大速率v分别为:( )
(2013?静安区二模)如图,质量为60g的铜棒长为d=20cm,棒的两端用长为L=30cm的细软铜线水平悬挂在磁感应强度为B=0.5T、方向竖直向上的匀强磁场中,当棒中通过恒定电流I后,铜棒向上摆动,最大偏角θ=60°,g取10m/s2,则铜棒中电流I和铜棒在摆动过程中的最大速率v分别为:( )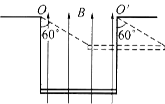
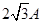 .
.
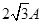 .
.