题目内容
 (2013?静安区二模)如图,质量为60g的铜棒长为d=20cm,棒的两端用长为L=30cm的细软铜线水平悬挂在磁感应强度为B=0.5T、方向竖直向上的匀强磁场中,当棒中通过恒定电流I后,铜棒向上摆动,最大偏角θ=60°,g取10m/s2,则铜棒中电流I和铜棒在摆动过程中的最大速率v分别为:( )
(2013?静安区二模)如图,质量为60g的铜棒长为d=20cm,棒的两端用长为L=30cm的细软铜线水平悬挂在磁感应强度为B=0.5T、方向竖直向上的匀强磁场中,当棒中通过恒定电流I后,铜棒向上摆动,最大偏角θ=60°,g取10m/s2,则铜棒中电流I和铜棒在摆动过程中的最大速率v分别为:( )分析:铜棒最大偏角是60°,则偏角为30°时是它的平衡位置,对铜棒受力分析,求出重力与安培力间的关系;偏角为30°时,铜棒的速度最大,由动能定理及安培力公式可以求出电流和最大速率.
解答:解:铜棒上摆的过程,根据动能定理得:
FBLsin60°-mgL(1-cos60°)=0,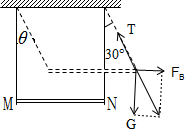
又安培力FB=BId
代入解得,I=2
A
由题意,铜棒向上摆动的最大偏角θ=60°,根据对称性可知,偏角是30°时是其平衡位置,铜棒受力如图所示,则有
G=FBcot30°=
FB ,
当铜棒偏角是30°时,速度最大,动能最大,
由动能定理可得:
m
=FBLsin30°-mgL(1-cos30°)
代入解得,最大速度vm=≈1m/s.
故选BC
FBLsin60°-mgL(1-cos60°)=0,

又安培力FB=BId
代入解得,I=2
| 3 |
由题意,铜棒向上摆动的最大偏角θ=60°,根据对称性可知,偏角是30°时是其平衡位置,铜棒受力如图所示,则有
G=FBcot30°=
| 3 |
当铜棒偏角是30°时,速度最大,动能最大,
由动能定理可得:
| 1 |
| 2 |
| v | 2 m |
代入解得,最大速度vm=≈1m/s.
故选BC
点评:知道偏角为30°位置是铜棒的平衡位置,对铜棒进行受力分析,熟练应用动能定理即可正确解题.

练习册系列答案
相关题目
 (2013?静安区二模)如图,两根互相平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、o、b在M、N的连线上,o为MN的中点,c、d位于MN的中垂线上,且a、b、c、d到o点的距离均相等.关于以上几点处的磁场,下列说法正确的是( )
(2013?静安区二模)如图,两根互相平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、o、b在M、N的连线上,o为MN的中点,c、d位于MN的中垂线上,且a、b、c、d到o点的距离均相等.关于以上几点处的磁场,下列说法正确的是( ) (2013?静安区二模)在“研究电磁感应现象”的实验中,首先按右上图接线,以查明电流表指针的偏转方向与电流方向之间的关系.当闭合S时观察到电流表指针向左偏,不通电时电流表指针停在正中央.然后按如图所示将电流表与线圈B连成一个闭合回路,将线圈A、电池、滑动变阻器和电键S串联成另一个闭合电路.
(2013?静安区二模)在“研究电磁感应现象”的实验中,首先按右上图接线,以查明电流表指针的偏转方向与电流方向之间的关系.当闭合S时观察到电流表指针向左偏,不通电时电流表指针停在正中央.然后按如图所示将电流表与线圈B连成一个闭合回路,将线圈A、电池、滑动变阻器和电键S串联成另一个闭合电路. (2013?静安区二模)如图所示为研究某未知元素放射性的实验装置,实验开始时在薄铝片和荧光屏之间有图示方向的匀强电场E,通过显微镜可以观察到,在荧光屏的某一位置上每分钟闪烁的亮点数.若撤去电场后继续观察,发现每分钟闪烁的亮点数没有变化;如果再将薄铝片移开,观察到每分钟闪烁的亮点数大大增加,由此可以判断,放射源发出的射线可能为( )
(2013?静安区二模)如图所示为研究某未知元素放射性的实验装置,实验开始时在薄铝片和荧光屏之间有图示方向的匀强电场E,通过显微镜可以观察到,在荧光屏的某一位置上每分钟闪烁的亮点数.若撤去电场后继续观察,发现每分钟闪烁的亮点数没有变化;如果再将薄铝片移开,观察到每分钟闪烁的亮点数大大增加,由此可以判断,放射源发出的射线可能为( )