题目内容
8.如图1所示,为“探究加速度与力、质量的关系”实验装置及数字化信息系统获得了小车加速度a与钩码的质量及小车和砝码的质量对应关系图.钩码的质量为m1,小车和砝码的质量为m2,重力加速度为g.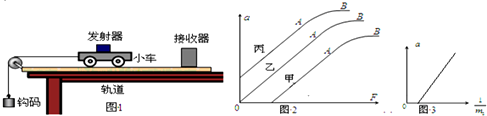
(1)下列说法正确的是D.
A.每次在小车上加减砝码时,应重新平衡摩擦力
B.实验时若用打点计时器应先释放小车后接通电源
C.本实验m2应远小于m1
D.在用图象探究加速度与质量关系时,应作$a-\frac{1}{m_2}$图象
(2)实验时,某同学由于疏忽,遗漏了平衡摩擦力这一步骤,测得F=m1g,作出a-F图象,他可能作出图2中甲 (选填“甲”、“乙”、“丙”)图线.此图线的AB段明显偏离直线,造成此误差的主要原因是D.
A.小车与轨道之间存在摩擦 B.导轨保持了水平状态
C.钩码的质量太大 D.所用下车和砝码的质量太大
(3)实验时,某同学遗漏了平衡摩擦力这一步骤,若轨道水平,他测量得到的$a-\frac{1}{m_2}$图象,如图3.设图中直线的斜率为k,在纵轴上的截距为b,则小车与木板间的动摩擦因数μ=$\frac{b}{g}$,钩码的质量m1=$\frac{k}{g}$.
(4)实验中打出的纸带如图4所示.相邻计数点间的时间是0.1s,其中x1=7.05cmx2=7.68cmx3=8.33cmx4=8.95cmx5=9.61cm,x6=10.26cm,由此可以算出小车运动的加速度是0.64m/s2.(结果保留两位有效数字)

分析 (1)实验时需要提前做的工作有两个:①平衡摩擦力,且每次改变小车质量时,不用重新平衡摩擦力,因为f=mgsinθ=μmgcosθ,m约掉了.②让小车的质量M远远大于小盘和重物的质量m.
(2)如果没有平衡摩擦力的话,就会出现当有拉力时,物体不动的情况.得出图象弯曲的原因是:未满足沙和沙桶质量远小于小车的质量.
(3)根据牛顿第二定律,列出小车的滑动摩擦力大小,然后结合图象的斜率与截距,可以得出结论.
(4)根据连续相等时间内的位移之差是一恒量求出加速度.
解答 解:(1)A、平衡摩擦力,假设木板倾角为θ,则有:f=mgsinθ=μmgcosθ,m约掉了,每次在小车上加减砝码时,故不需要重新平衡摩擦力.故A错误.
B、实验时应先接通电源后释放小车,故B错误.
C、让小车的质量m1远远大于小盘和重物的质量m2,因为:际上绳子的拉力F=m2a=$\frac{{m}_{1}g}{1+\frac{{m}_{1}}{{m}_{2}}}$,
故应该是m1<<m2,故C错误;
D、F=ma,所以:a=$\frac{F}{m}$,所以在用图象探究小车的加速度与质量的关系时,通常作a-$\frac{1}{{m}_{2}}$图象,故D正确;
故选:D
(2)遗漏了平衡摩擦力这一步骤,就会出现当有拉力时,物体不动的情况.故图线为甲.
当不满足m1<<m2时,随m1的增大物体的加速度a逐渐减小,故图象弯曲的原因是:所挂钩码的总质量太大,不满足钩码的质量远小于小车的质量,故C正确.
故选:C
(3)根据牛顿第二定律可知,m1g-μm2g=m2a;
结合a-$\frac{1}{{m}_{2}}$图象,可得:$\frac{1}{{m}_{2}}$=$\frac{μ}{{m}_{1}}+\frac{1}{{m}_{1}g}a$,
设图中直线的斜率为k,在纵轴上的截距为b,
因此钩码的质量m1=$\frac{k}{g}$,
小车与木板间的动摩擦因数μ=$\frac{b}{g}$.
(3)根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,得:
x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值,得:
a=$\frac{1}{3}$(a1+a2+a3)
即小车运动的加速度计算表达式为:a=$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$=$\frac{0.0895+0.0961+0.1026-0.0833-0.0768-0.0705}{0.09}$=0.64m/s2.
故答案为:(1)D;(2)甲,C (3)$\frac{b}{g}$,$\frac{k}{g}$(4)0.64
点评 会根据实验原理分析分析为什么要平衡摩擦力和让小车的质量M远远大于小桶(及砝码)的质量m,且会根据原理分析实验误差,同时掌握由牛顿第二定律列出方程,与图象的斜率与截距综合求解的方法.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案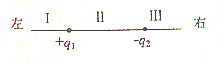 如图所示,位于同一直线上的两点电荷+q1和-q2将该直线划分成Ⅰ、Ⅱ、Ⅲ三个区域,另有一正的点电荷q0,设q0对+q1、-q2的电场的影响可忽略 不计,则( )
如图所示,位于同一直线上的两点电荷+q1和-q2将该直线划分成Ⅰ、Ⅱ、Ⅲ三个区域,另有一正的点电荷q0,设q0对+q1、-q2的电场的影响可忽略 不计,则( )| A. | 在Ⅰ区中,q0受力可能向左,也可能向右 | |
| B. | 在Ⅱ区中,q0受力可能向左,也可能向右 | |
| C. | 在Ⅲ区中,q0受力可能向左,也可能向右 | |
| D. | 在Ⅰ,Ⅲ区中,q0受力必定向左,在Ⅱ区中,q0受力必定向右 |
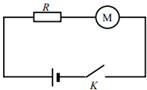 如图所示,一个电阻R和一个电动机M串联接在电动势为E,内电阻为r的直流电源上,电路中的电流为I,电动机正常转动,电阻R两端的电压为U1,电功率为P1,电动机两端的电压为U2,电功率为P2,则下列关系式正确的是( )
如图所示,一个电阻R和一个电动机M串联接在电动势为E,内电阻为r的直流电源上,电路中的电流为I,电动机正常转动,电阻R两端的电压为U1,电功率为P1,电动机两端的电压为U2,电功率为P2,则下列关系式正确的是( )| A. | P1=EI | B. | P2=U2I | C. | U1=E•Ir | D. | U2=IR |
 a、b、c三个α粒子(重力不计)由同一点M同时垂直场强方向进入带有等量异种电荷的两平行金属板的电场间,其轨迹如图所示,其中b恰好沿板的边缘飞出电场,由此可知( )
a、b、c三个α粒子(重力不计)由同一点M同时垂直场强方向进入带有等量异种电荷的两平行金属板的电场间,其轨迹如图所示,其中b恰好沿板的边缘飞出电场,由此可知( )| A. | 进入电场时a的速度最大,c的速度最小 | |
| B. | a、b、c在电场中运动经历的时间相等 | |
| C. | 若把上极板向上移动,则a在电场中运动经历的时间增长 | |
| D. | 若把下极板向下移动,则a在电场中运动经历的时间增长 |
| A. | 第2s的平均速度为15m/s | |
| B. | 后一秒的位移总比前一秒的位移多5m | |
| C. | 前 一秒的平均速度总比后一秒的平均速度小10m/s | |
| D. | 第7s的位移为65m |
 在平直的公路上,汽车启动后在第10s末,速度表的指针指在如图所示的位置,前10s内汽车运动的距离为150m.下列说法中正确的是( )
在平直的公路上,汽车启动后在第10s末,速度表的指针指在如图所示的位置,前10s内汽车运动的距离为150m.下列说法中正确的是( )| A. | 第10 s末汽车的瞬时速度是70 km/h | |
| B. | 第10 s末汽车的瞬时速度是70 m/s | |
| C. | 前10 s内汽车的平均速度是15 m/s | |
| D. | 前10 s内汽车的平均速度是35 m/s |