��Ŀ����
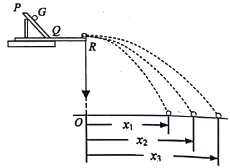
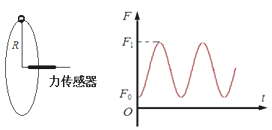
����Ŀ��Ϊ��̽��һδ֪�����Ա�ȼ�ʻ�ɴ����Ƹ�������渽������һ�ܣ������ʱΪT��Ȼ��ɴ����ٽ����ڸ����������Ա�ڷɴ�����ͼ����ʾװ��������Ϊm��С����ϸ�ߴ�������ֱ�������뾶ΪR��Բ���˶����������������ϸ���ϵ�������ʱ��仯�Ĺ�ϵ��ͼ�ң���֪������������ΪG���ɴ˿������������
A. �����������![]()
B. ��������ܶ�![]()
C. �����������������ٶ�![]()
D. ������ĵ�һ�����ٶ�![]()
���𰸡�BC
��������
�������������ṩ������![]() ��������r�����ǰ뾶������ɵø�����������������ܶȵĶ���
��������r�����ǰ뾶������ɵø�����������������ܶȵĶ���![]() ���������ݿ��Լ����������ܶȣ�С������ֱƽ������Բ���˶�������͵����ߵ㣬�����ṩ�������ֱ���ʽ���ٶȣ��ٸ��ݶ��ܶ�����ʽ�����������ٶȣ���һ�����ٶȵ������������������е����ǵ������ٶȣ����������ṩ������mg��m
���������ݿ��Լ����������ܶȣ�С������ֱƽ������Բ���˶�������͵����ߵ㣬�����ṩ�������ֱ���ʽ���ٶȣ��ٸ��ݶ��ܶ�����ʽ�����������ٶȣ���һ�����ٶȵ������������������е����ǵ������ٶȣ����������ṩ������mg��m![]() ���������ݻ���ɵø�����ĵ�һ�����ٶȣ�
���������ݻ���ɵø�����ĵ�һ�����ٶȣ�
�������������ṩ������![]() ���ø����������
���ø����������![]() ������Ŀ��û�н�������İ뾶r������С��Բ���˶��İ뾶ΪR����A������������V= 4��R3/3���ʸ�������ܶ�Ϊ
������Ŀ��û�н�������İ뾶r������С��Բ���˶��İ뾶ΪR����A������������V= 4��R3/3���ʸ�������ܶ�Ϊ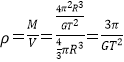 ����B��ȷ��С������ֱƽ������Բ���˶�������͵㣬�����ṩ������F1mg��
����B��ȷ��С������ֱƽ������Բ���˶�������͵㣬�����ṩ������F1mg��![]() ----��
----��
����ߵ㣬�����ṩ������F0+mg��![]() ----��
----��
����ߵ㵽��͵�Ĺ����У��˶����ܶ���mg2R��![]() mv��2
mv��2![]() mv��2----��
mv��2----��
�������Ϣ٢ڢ�ʽ���ɵø����������������ٶ�![]() ����C��ȷ����һ�����ٶȵ������������������е����ǵ������ٶȣ����������ṩ������mg��
����C��ȷ����һ�����ٶȵ������������������е����ǵ������ٶȣ����������ṩ������mg��![]() ���ø�����ĵ�һ�����ٶ�
���ø�����ĵ�һ�����ٶ�![]() ����D����ѡBC��
����D����ѡBC��

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�