题目内容
18.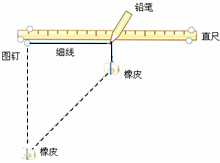 取一块橡皮,用一根细线拴住,把线的另一端用图钉固定在竖直放置的图板上.按如图所示的方法,用铅笔靠着线的一侧,沿直尺向右匀速移动,观察研究橡皮的运动情况.
取一块橡皮,用一根细线拴住,把线的另一端用图钉固定在竖直放置的图板上.按如图所示的方法,用铅笔靠着线的一侧,沿直尺向右匀速移动,观察研究橡皮的运动情况.(1)当铅笔沿直尺向右匀速移动时,橡皮在水平和竖直方向上各做什么运动?
(2)为了证明橡皮在竖直方向上分运动的性质,需要测量那些物理量(用字母表示),并用所测量的物理量表示水平和竖直方向的速度υx和υy.
(3)橡皮实际做什么运动?写出橡皮合速度υ的表达式(用测量的物理量表示).
分析 由于铅笔的作用,橡皮同时做水平向右的分运动和竖直向上的分运动,由运动的合成可知合速度的情况.
解答 解:(1)橡皮参与了水平向右和竖直向上的分运动,如图所示,两个方向的分运动都是匀速直线运动,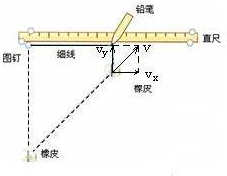
(2)因沿直尺向右匀速移动,且可读出移动的位移x,
再使用直尺测量出橡皮实验运动的位移s,及竖直方向的位移y,
根据三角知识,它们的位移是否满足s=$\sqrt{{x}^{2}+{y}^{2}}$;
若符合条件,则说明合运动是匀速直线运动,因此竖直方向是做匀速直线运动;
由运动学公式,则有:υx=$\frac{x}{t}$,υy=$\frac{y}{t}$,t是橡皮运动的时间;
(3)橡皮实际做匀速直线运动,橡皮合速度υ=$\sqrt{(\frac{x}{t})^{2}+(\frac{y}{t})^{2}}$;
答:(1)当铅笔沿直尺向右匀速移动时,橡皮在水平和竖直方向上各做匀速直线运动;
(2)需要测量测量出橡皮实验运动的位移s,及竖直方向的位移y,与运动的时间t,那么υx=$\frac{x}{t}$,υy=$\frac{y}{t}$.
(3)橡皮实际做匀速直线运动,写出橡皮合速度υ=$\sqrt{(\frac{x}{t})^{2}+(\frac{y}{t})^{2}}$.
点评 本题注意铅笔对线的运动,导致铅笔同时参与了两个运动,一个是向右的水平匀速运动,一个是向上的匀速运动,并掌握运动学公式的应用.

练习册系列答案
相关题目
8.质点做直线运动的v-t图象如图所示,则下列说法正确的是( )
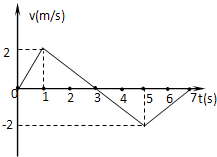

| A. | 质点前7秒的平均速度大小为1m/s | |
| B. | 第1秒内质点加速度大小是第5秒内加速度大小的2倍 | |
| C. | 1秒末质点的速度方向发生变化 | |
| D. | 3秒末质点回到出发点 |
9.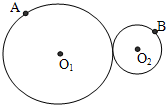 如图所示,A、B两点分别位于大、小轮的边缘上,rA:rB=2:1,它们之间靠摩擦传动,接触面上没有滑动.两轮在转动过程中,下列说法正确的是( )
如图所示,A、B两点分别位于大、小轮的边缘上,rA:rB=2:1,它们之间靠摩擦传动,接触面上没有滑动.两轮在转动过程中,下列说法正确的是( )
 如图所示,A、B两点分别位于大、小轮的边缘上,rA:rB=2:1,它们之间靠摩擦传动,接触面上没有滑动.两轮在转动过程中,下列说法正确的是( )
如图所示,A、B两点分别位于大、小轮的边缘上,rA:rB=2:1,它们之间靠摩擦传动,接触面上没有滑动.两轮在转动过程中,下列说法正确的是( )| A. | A、B两点的周期之比为1:2 | B. | A、B两点的向心加速度之比为1:2 | ||
| C. | A、B两点的角速度之比为1:1 | D. | A、B两点的线速度大小之比为2:1 |
13.质量为1.0kg的物体,在半径为2m的圆周上以2m/s的速度作匀速圆周运动.它需要的向心力大小为( )
| A. | 0.5N | B. | 1.0 N | C. | 2.0 N | D. | 4.0 N |
3.两个可视为点电荷的相同带电金属球,其电荷量之比为1:7,将它们接触后再放回原位置,两者间的相互作用的库仑力可能为原来的( )
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{16}{7}$ |
10.一辆汽车在平直公路上以额定功率行驶,设所受阻力不变.在汽车加速过程中( )
| A. | 牵引力减小,速度增大 | B. | 牵引力减小,加速度增大 | ||
| C. | 牵引力增大,速度减小 | D. | 牵引力增大,加速度减小 |
8.根据分子动理论判断以下关于分子力和分子势能的说法中正确的是( )
| A. | 当分子间距离为平衡距离r0时,分子具有最大势能 | |
| B. | 当分子间距离为平衡距离r0时,分子具有最小势能 | |
| C. | 当分子间距离为平衡距离r0时,引力和斥力都是最大值 | |
| D. | 当分子间距离为平衡距离r0时,引力和斥力都是零 |
 某实验小组利用图示实验装置来测量物块A和长木板之间的动摩擦因数μ.
某实验小组利用图示实验装置来测量物块A和长木板之间的动摩擦因数μ.