题目内容
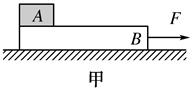
如图甲所示，倾角为θ的足够长的传送带以恒定的速率v0沿逆时针方向运行。t=0时，将质量m=1kg的物体（可视为质点）轻放在传送带上，物体相对地面的v-t图象如图乙所示。设沿传送带向下为正方向，取重力加速度g=10m/s2。则（ ）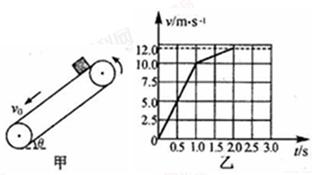
| A．传送带的速率v0=12m/s |
| B．传送带的倾角θ=30° |
| C．物体与传送带之间的动摩擦因数µ=0.4 |
| D．0～2.0s摩擦力对物体做功Wf="–24J" |
D
解析试题分析：物体先做初速度为零的匀加速直线运动，速度达到传送带速度后，由于重力沿斜面向下的分力大于摩擦力，物块继续向下做匀加速直线运动，从图象可知传送带的速度为10m/s，故A错误；开始时物体摩擦力方向沿斜面向下，速度相等后摩擦力方向沿斜面向上，则a1＝10m/s2，且满足mgsinθ+μmgcosθ=ma1；a1＝1m/s2，且满足mgsinθ-μmgcosθ=ma2；联立两式解得μ=0.5，θ=37°．故BC错误；第一段匀加速直线运动的位移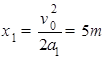
，摩擦力做功为Wf1=μmgcosθ?x1=0.5×10×0.8×5J=20J，第二段匀加速直线运动的位移
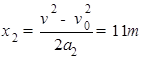，摩擦力做功为Wf2=-μmgcosθ?x2=-0.5×10×0.8×11J=-44J，所以Wf＝Wf1+Wf2＝20?44＝?24J．故D正确．
考点：牛顿第二定律的应用；摩擦力的功。
假想一个登陆舱接近了木星的一个卫星——木卫四的表面。如果发动机提供了一个3260N的向上的推力，登陆舱以恒定速率下降。如果发动机仅提供2200N的推力，登陆舱以0.4m/s2的加速度下降。则登陆舱的质量与靠近木卫四表面的自由下落的加速度分别为
| A．326kg 1.23m/s2 | B． 2650kg 2.46 m/s2 |
| C．2650kg 1.23m/s2 | D． 326kg 2.46.m/s2 |
如图所示，空间存在着与圆台母线垂直向外的磁场，各处的磁感应强度大小均为B，圆台母线与竖直方向的夹角为θ，一个质量为m、半径为r的匀质金属环位于圆台底部。环中维持恒定的电流I不变，圆环由静止向上运动，经过时间t后撤去该恒定电流并保持圆环闭合，圆环全程上升的最大高度为H。已知重力加速度为g，磁场的范围足够大。在圆环向上运动的过程中，下列说法正确的是（ ）
| A．在时间t内安培力对圆环做功为mgH |
| B．圆环先做匀加速运动后做匀减速运动 |
C．圆环运动的最大速度为 －gt |
| D．圆环先有扩张后有收缩的趋势 |
某同学在“验证牛顿运动定律”的实验中，保持小车所受的合力F的大小不变，改变小车的质量m，得到了不同m时的加速度大小a，并绘出了a?1/m 的图象，则（ ）
| A．图像是一条直线，直线的斜率表示小车受到的合力的倒数 |
| B．图像是一条直线，直线的斜率表示小车受到的合力 |
| C．图像是一条曲线，曲线各点的切线斜率表示小车受到的合力的倒数 |
| D．图像是一条曲线，曲线各点的切线斜率表示小车受到的合力 |
如图所示，倾角为30°的光滑杆上套有一个小球和两根轻质弹簧，两弹簧的一端各与小球相连，另一端分别用销钉Ｍ、Ｎ固定于杆上，小球处于静止状态．设拔去销钉Ｍ（撤去弹簧ａ）瞬间，小球的加速度大小为6ｍ/ｓ２．若不拔去销钉Ｍ，而拔去销钉Ｎ（撤去弹簧ｂ）瞬间，小球的加速度可能是（ｇ取10ｍ/ｓ２）：（ ）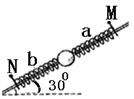
| A．11ｍ/ｓ２，沿杆向上 | B．11ｍ/ｓ２，沿杆向下 |
| C．1ｍ/ｓ２，沿杆向上 | D．1ｍ/ｓ２，沿杆向下 |
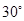，当升降机突然处于完全失重状态时，则此瞬时AB两物体的瞬时加速度为别为（ ）
、
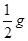B．
、
D．
