题目内容
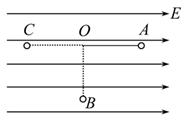
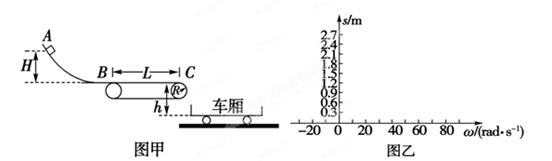
（18分）如图所示，一质量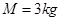
的足够长木板B静止于光滑水平面上，B的右边放有竖直挡板，B的右端距挡板
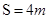.现有一小物体A（可视为质点）质量
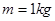，以初速度
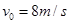从B的左端水平滑上B．已知A与B间的动摩擦因数
，B与竖直挡板的碰撞时间极短，且碰撞时无机械能损失.求：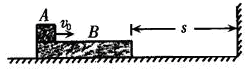
（1）B与竖直挡板相碰前的速度是多少？
（2）若题干中的S可以任意改变（S不能为零）大小，要使B第一次碰墙后，AB系统动量为零，S的大小是多少？
（3）若要求B与墙碰撞两次，B的右端距挡板S应该满足什么条件？
（1）
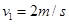（2）
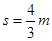（3）
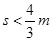
解析试题分析:（1）设A和B达到共同速度为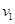
时，B向右运动距离为
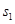，以AB整体为研究对象可知，AB组成的系统动量守恒有：
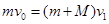，可得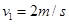
对B由动能定理有：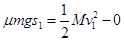
，联立解得：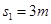
由于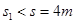
，可知B与挡板碰撞时，A、B已达到共同速度，则B的速度为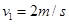
（2）设B与墙壁第一次碰前A、B的速度为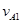
、
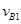，则：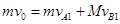
对B由动能定理有：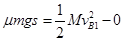
B与墙碰撞时无机械能损失，则B以速度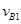反向运动；而A与B系统动量为零，故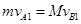
联立解得：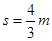
（3）设B与墙壁第一次碰前A、B的速度为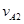
、
，
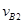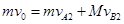
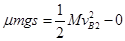
若要求B与墙碰撞两次则碰后系统的总动量仍向右，即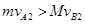
，
可得。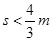
考点：本题考查了动量守恒定律、动能定理。
练习册系列答案
相关题目
