题目内容
17. (1)在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某人得到的记录纸分别如图所示,从图中明显看出实验错误是斜槽末端未调节水平,检测斜槽末端水平的方法是小球放在斜槽末端任意位置都能处于静止状态.
(1)在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某人得到的记录纸分别如图所示,从图中明显看出实验错误是斜槽末端未调节水平,检测斜槽末端水平的方法是小球放在斜槽末端任意位置都能处于静止状态.(2)在“研究平抛物体运动”的实验中,可以描绘平抛物体运动轨迹和求物体的平抛初速度.实验简要步骤如下:
A.让小球多次从静止、同一位置上滚下,记下小球穿过卡片孔的一系列位置;
B.安装好器材,注意斜槽末端水平和平板竖直,记下斜槽末端O点和过O点的竖直线.
C.测出曲线上某点的坐标x、y,用v0=x$\sqrt{\frac{g}{2y}}$算出该小球的平抛初速度,实验需要对多个点求v0的值,然后求它们的平均值.
D.取下白纸,以O为原点,以竖直线为轴建立坐标系,用平滑曲线画平抛轨迹.
上述实验步骤的合理顺序是BADC(只排列序号即可).
分析 让小球多次从同一位置上静止滚下,目的是保证小球多次做平抛运动的初速度相等.保证小球做平抛运动,所以斜槽末端保持水平;
平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动,根据平抛运动的特点即可求解.
实验步骤的合理顺序的排列要明确实验的正确安排顺序.
解答 解:(1)从图中明显看出实验错误是斜槽末端末调节水平,检测斜槽末端水平的方法是小球放在斜槽末端任意位置都能处于静止状态.
(2)A、为了保证小球的初速度相等,每次让小球从静止在同一位置滚下.
C、根据$y=\frac{1}{2}g{t}^{2}$,x=v0t得,${v}_{0}=x\sqrt{\frac{g}{2y}}$.
按照组装器材、进行实验、数据处理的顺序,操作步骤合理的顺序是BADC.
故答案为:(1)斜槽末端未调节水平,小球放在斜槽末端任意位置都能处于静止状态
(2)A.静止、同一
C.x$\sqrt{\frac{g}{2y}}$.
顺序:BADC
点评 关于平抛运动实验要掌握实验的注意事项、实验步骤、实验原理.平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动.分析小球水平方向和竖直方向的运动特点,充分利用匀变速直线运动的规律结合运动的合成来求解.

练习册系列答案
相关题目
7.下列说法正确的是( )
| A. | “搓搓手就感觉手暖和些”是通过会热传递来改变物体内能 | |
| B. | 在热传递过程中,内能多的物体其内能将减少,内能少的物体其内能将增加,直到两个物体的内能相等 | |
| C. | 一个系统与另一个系统是否达到热平衡状态取决于温度 | |
| D. | 0℃水的内能比0℃的内能多 |
12.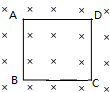 如图所示,匀强磁场垂直于纸面向里,场强大小为B,边长为L的正方形线圈ABCD在纸面内,现给线圈通以顺时针方向、强度大小为I的恒定电流,线圈形状不变,则线圈A点的张力为( )
如图所示,匀强磁场垂直于纸面向里,场强大小为B,边长为L的正方形线圈ABCD在纸面内,现给线圈通以顺时针方向、强度大小为I的恒定电流,线圈形状不变,则线圈A点的张力为( )
 如图所示,匀强磁场垂直于纸面向里,场强大小为B,边长为L的正方形线圈ABCD在纸面内,现给线圈通以顺时针方向、强度大小为I的恒定电流,线圈形状不变,则线圈A点的张力为( )
如图所示,匀强磁场垂直于纸面向里,场强大小为B,边长为L的正方形线圈ABCD在纸面内,现给线圈通以顺时针方向、强度大小为I的恒定电流,线圈形状不变,则线圈A点的张力为( )| A. | $\frac{\sqrt{2}}{2}$BIL | B. | BIL | C. | $\sqrt{2}$BIL | D. | 2BIL |
9. 氢原子的能级如图所示,一群氢原子处于n=3的激发态,在向基态跃迁的过程中,下列说法中正确的是( )
氢原子的能级如图所示,一群氢原子处于n=3的激发态,在向基态跃迁的过程中,下列说法中正确的是( )
 氢原子的能级如图所示,一群氢原子处于n=3的激发态,在向基态跃迁的过程中,下列说法中正确的是( )
氢原子的能级如图所示,一群氢原子处于n=3的激发态,在向基态跃迁的过程中,下列说法中正确的是( )| A. | 这群氢原子能发出三种频率不同的光,其中从n=3跃迁到n=1所发出光的波长最短 | |
| B. | 这群氢原子能发出两种频率不同的光,其中从n=3跃迁到n=1所发出光的波长最大 | |
| C. | 用这群氢原子所发的光照射逸出功为2.49eV的金属钠,则从金属钠表面所发出的光电子的最大初动能为11.11eV | |
| D. | 用这群氢原子所发的光照射逸出功为2.49eV的金属钠,则从金属钠表面所发出的光电子的最大初动能为9.60eV |
6. 如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以地面为零势能面且不计空气阻力,则下列说法中正确的是( )
如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以地面为零势能面且不计空气阻力,则下列说法中正确的是( )
 如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以地面为零势能面且不计空气阻力,则下列说法中正确的是( )
如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以地面为零势能面且不计空气阻力,则下列说法中正确的是( )| A. | 物体在地面时的机械能为mgh | |
| B. | 物体在地面时的机械能为$\frac{1}{2}$${mv}_{0}^{2}$ | |
| C. | 重力对物体做的功为mgh | |
| D. | 物体在海平面上的动能为$\frac{1}{2}$m${v}_{0}^{2}$+mgh |
7. 中国是世界上自行车产量最大和拥有量最多的国家,13亿多人口,就有4亿多辆自行车.某同学在平直的水平路面上匀速骑车,该同学所骑的自行车链轮的半径为R1,飞轮的半径为R2,后车轮的半径为R3,如图所示.该同学在t时间内,踩着脚踏板转了N圈(不间断地匀速蹬),且车轮与地面接触处都无滑动,则该同学的速率为( )
中国是世界上自行车产量最大和拥有量最多的国家,13亿多人口,就有4亿多辆自行车.某同学在平直的水平路面上匀速骑车,该同学所骑的自行车链轮的半径为R1,飞轮的半径为R2,后车轮的半径为R3,如图所示.该同学在t时间内,踩着脚踏板转了N圈(不间断地匀速蹬),且车轮与地面接触处都无滑动,则该同学的速率为( )
 中国是世界上自行车产量最大和拥有量最多的国家,13亿多人口,就有4亿多辆自行车.某同学在平直的水平路面上匀速骑车,该同学所骑的自行车链轮的半径为R1,飞轮的半径为R2,后车轮的半径为R3,如图所示.该同学在t时间内,踩着脚踏板转了N圈(不间断地匀速蹬),且车轮与地面接触处都无滑动,则该同学的速率为( )
中国是世界上自行车产量最大和拥有量最多的国家,13亿多人口,就有4亿多辆自行车.某同学在平直的水平路面上匀速骑车,该同学所骑的自行车链轮的半径为R1,飞轮的半径为R2,后车轮的半径为R3,如图所示.该同学在t时间内,踩着脚踏板转了N圈(不间断地匀速蹬),且车轮与地面接触处都无滑动,则该同学的速率为( )| A. | $\frac{2πN{R}_{2}{R}_{3}}{{R}_{1}•t}$ | B. | $\frac{2πN{R}_{2}{R}_{1}}{{R}_{3}•t}$ | C. | $\frac{2πN{R}_{1}{R}_{3}}{{R}_{2}•t}$ | D. | $\frac{2πN{R}_{3}}{{R}_{2}{R}_{1}•t}$ |
 用多用表的欧姆档测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆档调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.
用多用表的欧姆档测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆档调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.