题目内容
【题目】在如图所示宽度范围内,用场强为E的匀强电场可使初速度是v0的某种带正电粒子偏转θ角.在同样宽度范围内,若改用方向垂直于纸面向外的匀强磁场,使该粒子穿过该区域,并使偏转角也为θ(不计粒子的重力),问: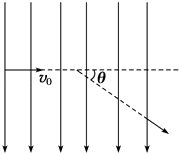
(1)匀强磁场的磁感应强度是多大?
(2)粒子穿过电场和磁场的时间之比是多大?
【答案】
(1)解:设粒子的质量m,电荷量q,场区宽度L,粒子在电场中做类平抛运动
t= ![]() ①
①
a= ![]() ②
②
tanθ= ![]() ③
③
由①②③得:tanθ= ![]() ④
④
粒子在磁场中做匀速圆周运动,轨迹如图所示.
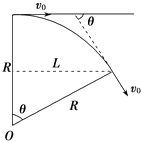
R= ![]() ⑤
⑤
由几何知识得:sinθ= ![]() ⑥
⑥
由⑤⑥解得:sinθ= ![]() ⑦
⑦
由④⑦式解得:B= ![]()
(2)解:粒子在电场中运动时间t1= ![]() ⑧
⑧
在磁场中运动时间t2= ![]() =
= ![]() ⑨
⑨
而L= ![]() ⑩,
⑩,
由⑧⑨⑩解出: ![]() =
= ![]()
【解析】(1)正离子在电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速为零的匀加速直线运动,由牛顿第二定律和运动学公式结合得到偏转角正切tanθ的表达式.在磁场中,离子由洛伦兹力提供向心力,由几何知识求出半径,由牛顿第二定律求出sinθ.联立即可求得磁感应强度.(2)离子穿过电场时,由水平方向的运动位移和速度求出时间.在磁场中,由t= ![]() T求出时间,即可得解.
T求出时间,即可得解.

练习册系列答案
相关题目