题目内容
【题目】如图所示，一定质量的气体放在体积为V0的容器中，室温为T0＝300 K，有一光滑导热活塞C(不占体积)将容器分成A、B两室，B室的体积是A室的两倍，A室容器上连接有一U形管(U形管内气体的体积忽略不计)，两边水银柱高度差为76 cm，右室容器中连接有一阀门K，可与大气相通(外界大气压等于76 cmHg)求：
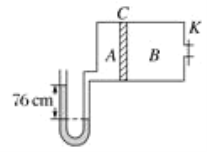
(1)将阀门K打开后，A室的体积变成多少？
(2)打开阀门K后将容器内的气体从300 K分别加热到400 K和540 K时，U形管内两边水银面的高度差各为多少？
【答案】(1) 
(2) 0 15．2 cm
【解析】本题考查理想气体的状态方程。
(1)开始时， 
， 
打开阀门，A室气体等温变化， 
，体积为
由玻意耳定律得
得
(2)设打开阀门后将容器内气体从T0＝300 K升到T，体积由
变到V0，气体发生等压变化．
由盖—吕萨克定律得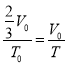
，即
因T1＝400 K<450 K，气体压强为
，故水银柱高度差为0．
从T＝450 K升高到T2＝540 K过程中，气体发生等容变化．
由查理定律
得
T2＝540 K时，水银面的高度差为(1．2－1)×76 cm＝15．2 cm．
练习册系列答案
教材全解字词句篇系列答案
相关题目
